ACER

Overview

ACER, short for actor-critic with experience replay, presents an actor-critic deep reinforcement learning agent with experience replay that is stable, sample efficient, and performs remarkably well on challenging environments, including the discrete 57-game Atari domain and several continuous control problems. It greatly increases the sample efficiency and decreases the data correlation by using the following tricks:

• Truncated importance sampling with bias correction, which controls the stability of the off-policy estimator

• Retrace Q value estimation, which is an off-policy, low variance, and return-based algorithm, and has been proven to converge

• Efficient TRPO (Trust Region Policy Optimization), which scales well to large problems

• Stochastic Dueling Networks (SDNs), which is designed to estimate both \(V^\pi\) and \(Q^\pi\) off-policy while maintaining consistency between the two estimates

You can find more details in the paper Sample Efficient Actor-Critic with Experience Replay.

Quick Facts

1. ACER is a model-free and off-policy RL algorithm.

2. ACER supports both discrete action spaces and continuous action spaces with several differences.

3. ACER is an actor-critic RL algorithm, which optimizes the actor and critic networks respectively.

4. ACER decouples acting from learning. Collectors in ACER need to record behavior probability distributions.

In the following sections, we take the discrete case as an example to elaborate on ACER algorithm.

Key Equations

Loss used in ACER contains policy loss and value loss. They are updated separately, so it’s necessary to control their relative update speeds.

Retrace Q-value estimation

Given a trajectory generated under the behavior policy \(\mu\), we retrieve a trajectory \({x_0, a_0, r_0, \mu(\cdot|x_0),..., x_k, a_k, r_k, \mu(\cdot|x_k)}\) the Retrace estimator can be expressed recursively as follows:

\[Q^{\text{ret}}(x_t,a_t)=r_t+\gamma\bar{\rho}_{t+1}[Q^{\text{ret}}(x_{t+ 1},a_{t+1})]+\gamma V(x_{t+1})\]

where \(\bar{\rho}_t\) is the truncated importance weight, \(\bar{\rho}_t=\min\{c,\rho\}\) with \(\frac{\pi(a_t|x_t)}{\mu(a_t|x_t)}\). \(\pi\) is the target policy. Retrace is an off-policy, return based algorithm which has low variance and is proven to converge to the value function of the target policy for any behavior policy. We approximate the Q value by neural network \(Q_{\theta}\). We use a mean squared error loss:

\[{\text{value}}=\frac{1}{2}(Q^{\text{ret}}(x_t,a_t)-Q_{\theta}(x_t,a_t))^2.\]

Policy Gradient

To safe-guard against high variance, ACER uses truncated importance weights and introduces correction term via the following decomposition of \(g^{acer}\):

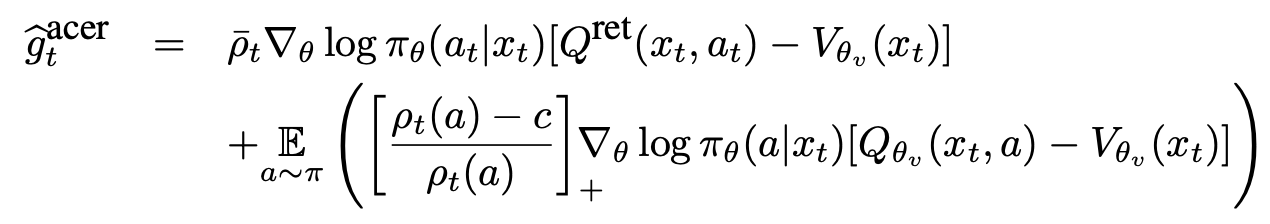
To ensure stability, ACER limits the per-step change to the policy by solving the following linearized KL divergence constraint:

\[\begin{split}\begin{split} &\text{minimize}_z\quad\frac{1}{2}\|g_t^{\text{acer}}-z\|_2^2\\ &subjec\ to\quad \nabla_{\phi_{\theta}(x_t)}D_{KL}[f(\cdot|\phi_{\theta_a}(x_t))\|f(\cdot|\phi_{\theta}(x_t))]^\top\le\delta \end{split}\end{split}\]

The \(\phi(\theta)\) is the target policy network and the \(\phi(\theta_a)\) is the average policy network. By letting \(k=\nabla_{\phi_{\theta}(x_t)}D_{KL}[f(\cdot|\phi_{\theta_a}(x_t))\|f(\cdot|\phi_{\theta}(x_t))]\), the solution can be easily derived in closed form using the KKT condition:

\[z^*=g_{t}^{\text{acer}}-\max\{0,\frac{k^\top g_t^{\text{acer}}-\delta}{\|k\|_2^2}\}k\]

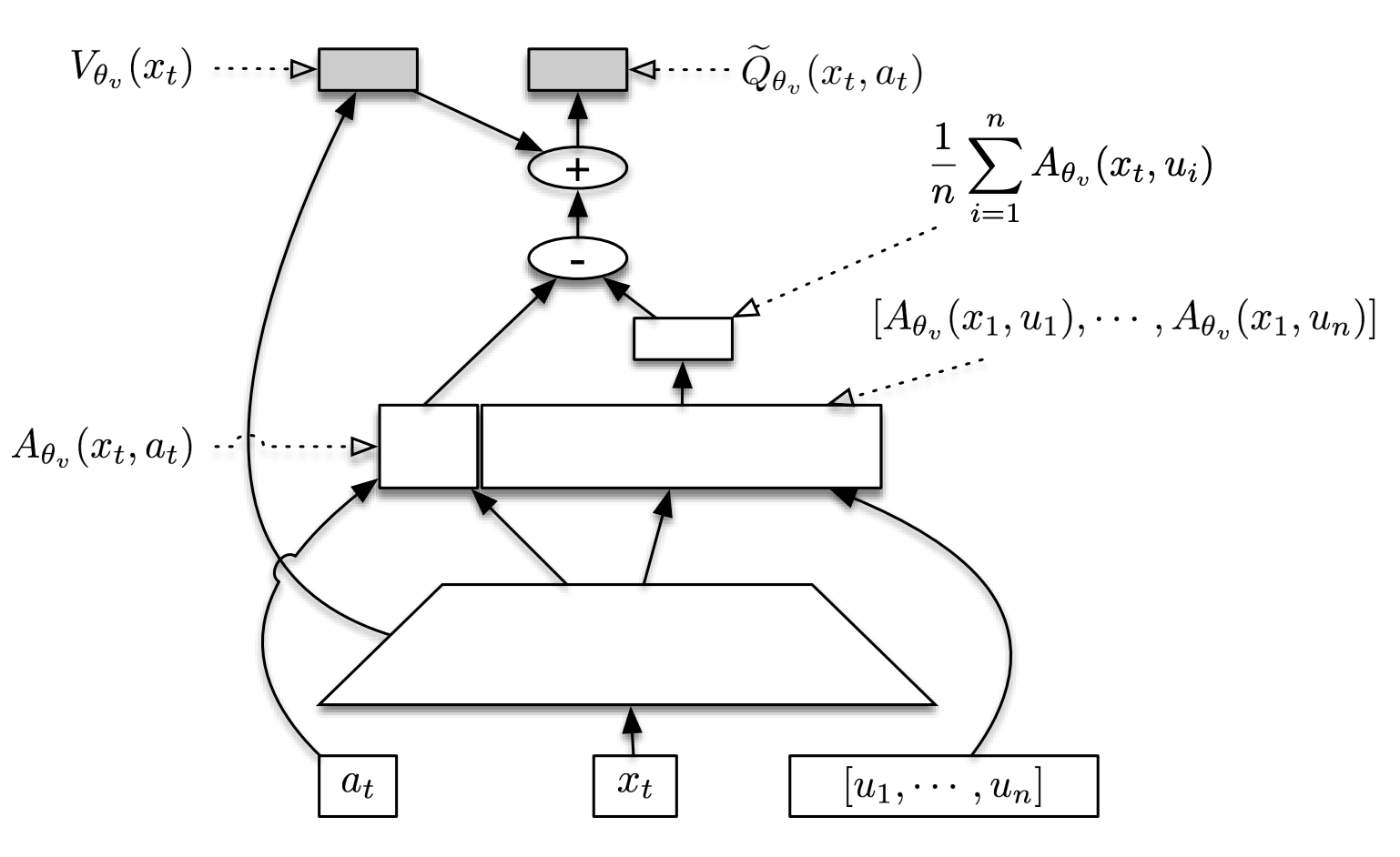
Key Graph or Network Structure

The following graph depicts the SDN structure (picture from paper Sample Efficient Actor-Critic with Experience Replay). In the drawing, \([u_1, .... , u_n]\) are assumed to be samples from \(\pi_\theta(·|x_t)\).

Pseudo-code

There are a few changes between ACER applied to discrete action spaces and that applied to continuous action space.

In continuous action space, it is impossible to enumerate Q values for every action. So ACER uses the sampled actions to approximate the expected value.

Implementations

Here we show the ACER algorithm on the discrete action space. The default config is defined as follows:

class ding.policy.acer.ACERPolicy(cfg: EasyDict, model: Module | None = None, enable_field: List[str] | None = None)

Overview:

Policy class of ACER algorithm.

Config:

ID	Symbol	Type	Default Value	Description	Other(Shape)
1	type	str	acer	RL policy register name, refer to registry POLICY_REGISTRY	this arg is optional, a placeholder
2	cuda	bool	False	Whether to use cuda for network	this arg can be diff- erent from modes
3	on_policy	bool	False	Whether the RL algorithm is on-policy or off-policy
4	trust_region	bool	True	Whether the RL algorithm use trust region constraint
5	trust_region_value	float	1.0	maximum range of the trust region
6	unroll_len	int	32	trajectory length to calculate Q retrace target
7	learn.update per_collect	int	4	How many updates(iterations) to train after collector’s one collection. Only valid in serial training	this args can be vary from envs. Bigger val means more off-policy
8	c_clip_ratio	float	1.0	clip ratio of importance weights

Usually, we hope to compute everything as a batch to improve efficiency. This is done in policy._get_train_sample. Once we execute this function in collector, the length of samples will equal to unroll-len in config. For details, please refer to doc of ding.rl_utils.adder.

The whole code of ACER you can find here. Here we show some details of this algorithm.

First, we use the following functions to compute the retrace Q value.

def compute_q_retraces(
        q_values: torch.Tensor,
        v_pred: torch.Tensor,
        rewards: torch.Tensor,
        actions: torch.Tensor,
        weights: torch.Tensor,
        ratio: torch.Tensor,
        gamma: float = 0.9
) -> torch.Tensor:
    rewards = rewards.unsqueeze(-1)  # shape T,B,1
    actions = actions.unsqueeze(-1)  # shape T,B,1
    weights = weights.unsqueeze(-1)  # shape T,B,1
    q_retraces = torch.zeros_like(v_pred)  # shape (T+1),B,1
    n_len = q_retraces.size()[0]  # T+1
    tmp_retraces = v_pred[-1, ...]  # shape B,1
    q_retraces[-1, ...] = v_pred[-1, ...]
    q_gather = torch.zeros_like(v_pred)
    q_gather[0:-1, ...] = q_values[0:-1, ...].gather(-1, actions)  # shape (T+1),B,1
    ratio_gather = ratio.gather(-1, actions)  # shape T,B,1

    for idx in reversed(range(n_len - 1)):
        q_retraces[idx, ...] = rewards[idx, ...] + gamma * weights[idx, ...] * tmp_retraces
        tmp_retraces = ratio_gather[idx, ...].clamp(max=1.0) * (q_retraces[idx, ...] - q_gather[idx, ...]) + v_pred[idx, ...]
    return q_retraces  # shape (T+1),B,1

After that, we calculate the value of policy loss, it will calculate the actor loss with importance weights truncation and bias correction loss by the following function

def acer_policy_error(
        q_values: torch.Tensor,
        q_retraces: torch.Tensor,
        v_pred: torch.Tensor,
        target_logit: torch.Tensor,
        actions: torch.Tensor,
        ratio: torch.Tensor,
        c_clip_ratio: float = 10.0
) -> Tuple[torch.Tensor, torch.Tensor]:
    """
    Overview:
        Get ACER policy loss
    Arguments:
        - q_values (:obj:`torch.Tensor`): Q values
        - q_retraces (:obj:`torch.Tensor`): Q values (be calculated by retrace method)
        - v_pred (:obj:`torch.Tensor`): V values
        - target_pi (:obj:`torch.Tensor`): The new policy's probability
        - actions (:obj:`torch.Tensor`): The actions in replay buffer
        - ratio (:obj:`torch.Tensor`): ratio of new polcy with behavior policy
        - c_clip_ratio (:obj:`float`): clip value for ratio
    Returns:
        - actor_loss (:obj:`torch.Tensor`): policy loss from q_retrace
        - bc_loss (:obj:`torch.Tensor`): correct policy loss
    Shapes:
        - q_values (:obj:`torch.FloatTensor`): :math:`(T, B, N)`, where B is batch size and N is action dim
        - q_retraces (:obj:`torch.FloatTensor`): :math:`(T, B, 1)`
        - v_pred (:obj:`torch.FloatTensor`): :math:`(T, B, 1)`
        - target_pi (:obj:`torch.FloatTensor`): :math:`(T, B, N)`
        - actions (:obj:`torch.LongTensor`): :math:`(T, B)`
        - ratio (:obj:`torch.FloatTensor`): :math:`(T, B, N)`
        - actor_loss (:obj:`torch.FloatTensor`): :math:`(T, B, 1)`
        - bc_loss (:obj:`torch.FloatTensor`): :math:`(T, B, 1)`
    """
    actions = actions.unsqueeze(-1)
    with torch.no_grad():
        advantage_retraces = q_retraces - v_pred  # shape T,B,1
        advantage_native = q_values - v_pred  # shape T,B,env_action_shape
    actor_loss = ratio.gather(-1, actions).clamp(max=c_clip_ratio) * advantage_retraces * target_logit.gather(
        -1, actions
    )  # shape T,B,1

    # bias correction term, the first target_pi will not calculate gradient flow
    bias_correction_loss = (1.0-c_clip_ratio/(ratio+EPS)).clamp(min=0.0)*torch.exp(target_logit).detach() * \
        advantage_native*target_logit  # shape T,B,env_action_shape
    bias_correction_loss = bias_correction_loss.sum(-1, keepdim=True)
    return actor_loss, bias_correction_loss

Then, we execute backward operation towards target_pi. Moreover, we need to calculate the correction gradient in the trust region:

def acer_trust_region_update(
        actor_gradients: List[torch.Tensor], target_logit: torch.Tensor, avg_logit: torch.Tensor,
        trust_region_value: float
) -> List[torch.Tensor]:
    """
    Overview:
        calcuate gradient with trust region constrain
    Arguments:
        - actor_gradients (:obj:`list(torch.Tensor)`): gradients value's for different part
        - target_pi (:obj:`torch.Tensor`): The new policy's probability
        - avg_pi (:obj:`torch.Tensor`): The average policy's probability
        - trust_region_value (:obj:`float`): the range of trust region
    Returns:
        - update_gradients (:obj:`list(torch.Tensor)`): gradients with trust region constraint
    Shapes:
        - target_pi (:obj:`torch.FloatTensor`): :math:`(T, B, N)`
        - avg_pi (:obj:`torch.FloatTensor`): :math:`(T, B, N)`
    """
    with torch.no_grad():
        KL_gradients = [torch.exp(avg_logit)]
    update_gradients = []
    # TODO: here is only one elements in this list.Maybe will use to more elements in the future
    actor_gradient = actor_gradients[0]
    KL_gradient = KL_gradients[0]
    scale = actor_gradient.mul(KL_gradient).sum(-1, keepdim=True) - trust_region_value
    scale = torch.div(scale, KL_gradient.mul(KL_gradient).sum(-1, keepdim=True)).clamp(min=0.0)
    update_gradients.append(actor_gradient - scale * KL_gradient)
    return update_gradients

With the new gradients, we can continue to propagate backwardly and then update parameters accordingly.

Finally, we should calculate the mean squared loss for Q values to update Q-Network

def acer_value_error(q_values, q_retraces, actions):
    """
    Overview:
        Get ACER critic loss
    Arguments:
        - q_values (:obj:`torch.Tensor`): Q values
        - q_retraces (:obj:`torch.Tensor`): Q values (be calculated by retrace method)
        - actions (:obj:`torch.Tensor`): The actions in replay buffer
        - ratio (:obj:`torch.Tensor`): ratio of new polcy with behavior policy
    Returns:
        - critic_loss (:obj:`torch.Tensor`): critic loss
    Shapes:
        - q_values (:obj:`torch.FloatTensor`): :math:`(T, B, N)`, where B is batch size and N is action dim
        - q_retraces (:obj:`torch.FloatTensor`): :math:`(T, B, 1)`
        - actions (:obj:`torch.LongTensor`): :math:`(T, B)`
        - critic_loss (:obj:`torch.FloatTensor`): :math:`(T, B, 1)`
    """
    actions = actions.unsqueeze(-1)
    critic_loss = 0.5 * (q_retraces - q_values.gather(-1, actions)).pow(2)
    return

Benchmark

environment	best mean reward	evaluation results	config link	comparison
Pong (PongNoFrameskip-v4)	20		config_link_p
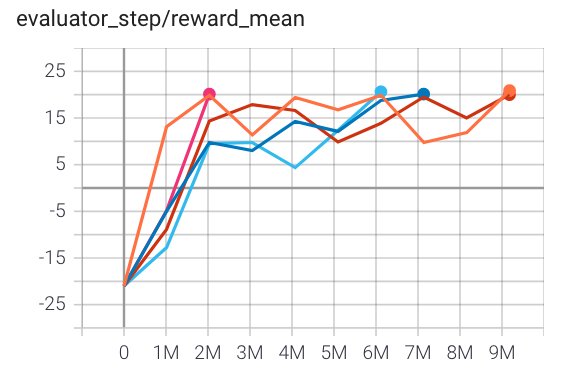
Qbert (QbertNoFrameskip-v4)	4000(todo)		config_link_q
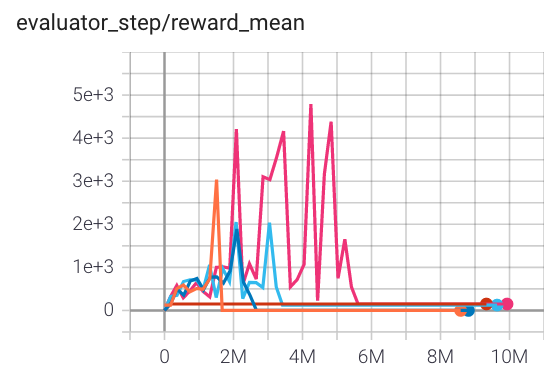
SpaceInvaders (SpaceInvadersNoFrame skip-v4)	1100		config_link_s

References

• Ziyu Wang, Victor Bapst, Nicolas Heess, Volodymyr Mnih, Remi Munos, Koray Kavukcuoglu, Nando de Freitas: “Sample Efficient Actor-Critic with Experience Replay”, 2016; [https://arxiv.org/abs/1611.01224 arxiv:1611.01224].

Other Public Implementations

• ACER

• chainerrl