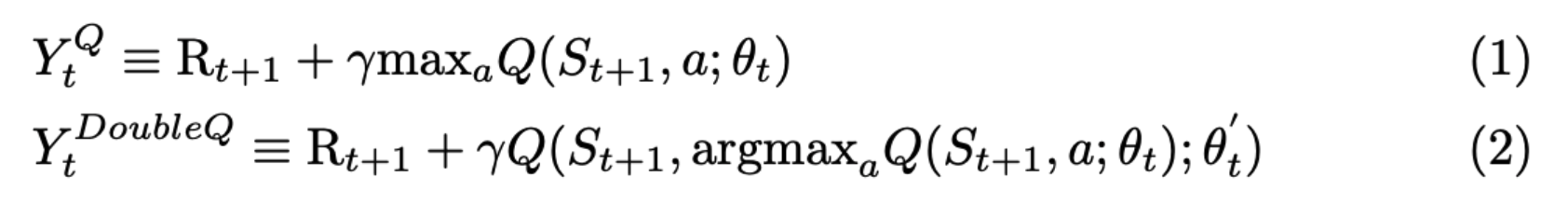DQN

Overview

DQN was proposed in Human-level control through deep reinforcement learning. Traditional Q-learning maintains an M*N Q value table (where M represents the number of states and N represents the number of actions), and iteratively updates the Q-value through the Bellman equation. This kind of algorithm will have the problem of dimensionality disaster when the state/action space becomes extremely large.

DQN is different from traditional reinforcement learning methods. It combines Q-learning with deep neural networks, uses deep neural networks to estimate the Q value, calculates the temporal-difference loss, and perform a gradient descent step to make an update. Two tricks that improves the training stability for large neural networks are experience replay and fixed target Q-targets. The DQN agent is able to reach a level comparable to or even surpass human players in decision-making problems in high-dimensional spaces (such as Atari games).

Quick Facts

1. DQN is a model-free and value-based RL algorithm.

2. DQN only support discrete action spaces.

3. DQN is an off-policy algorithm.

4. Usually, DQN uses eps-greedy or multinomial sampling for exploration.

5. DQN + RNN = DRQN.

6. The DI-engine implementation of DQN supports multi-discrete action space.

Key Equations or Key Graphs

The TD-loss used in DQN is:

\[\mathrm{L}(w)=\mathbb{E}\left[(\underbrace{r+\gamma \max _{a^{\prime}} Q_{\text {target }}\left(s^{\prime}, a^{\prime}, \theta^{-}\right)}-Q(s, a, \theta))^{2}\right]\]

where the target network \(Q_{\text {target }}\), with parameters \(\theta^{-}\), is the same as the online network except that its parameters are copied every target_update_freq steps from the online network (The hyper-parameter target_update_freq can be modified in the configuration file. Please refer to TargetNetworkWrapper for more details).

Pseudo-code

Note

Compared with the version published in Nature, DQN has been dramatically modified. In the algorithm parts, n-step TD-loss, PER and dueling head are widely used, interested users can refer to the paper Rainbow: Combining Improvements in Deep Reinforcement Learning .

Extensions

DQN can be combined with:

• PER (Prioritized Experience Replay)

  PER replaces the uniform sampling in a replay buffer with so-called priority defined by various metrics, such as absolute TD error, the novelty of observation and so on. By this priority sampling, the convergence speed and performance of DQN can be improved significantly.

  There are two ways to implement PER. One of them is described below:

  

  In DI-engine, PER can be enabled by modifying two fields priority and priority_IS_weight in the configuration file, and the concrete code can refer to PER code . For a specific example, users can refer to PER example

• Multi-step TD-loss

  In single-step TD-loss, the update of Q-learning (Bellman equation) is described as follows:

  \[r(s,a)+\gamma \max_{a^{'}}Q(s',a')\]

  While in multi-step TD-loss, it is replaced by the following formula:

  \[\sum_{t=0}^{n-1}\gamma^t r(s_t,a_t) + \gamma^n \max_{a^{'}}Q(s_n,a')\]

  Note

  An issue about n-step for Q-learning is that, when epsilon greedy is adopted, the q value estimation is biased because the \(r(s_t,a_t)\) at t>=1 are sampled under epsilon greedy rather than the policy itself. However, multi-step along with epsilon greedy generally improves DQN practically.

  In DI-engine, Multi-step TD-loss can be enabled by the nstep field in the configuration file, and the loss function is described in q_nstep_td_error in nstep code.

• Double DQN

  Double DQN, proposed in Deep Reinforcement Learning with Double Q-learning, is a common variant of DQN. The max operator in standard Q-learning and DQN when computing the target network uses the same Q values both to select and to evaluate an action. This makes it more likely to select overestimated values, resulting in overoptimistic value estimates. To prevent this, we can decouple the selection from the evaluation. More concretely, the difference is shown the the following two formula:

  The targets in Q-learning labelled by (1) and Double DQN labelled by (2) are illustrated as follows:

  

  Namely, the target network in Double DQN doesn’t select the maximum action according to the target network but first finds the action whose q_value is highest in the online network, then gets the q_value from the target network computed by the selected action. This variant can surpass the overestimation problem of target q_value, and reduce upward bias.

  In summary, Double Q-learning can suppress the over-estimation of Q value to reduce related negative impact.

  In DI-engine, Double DQN is implemented by default without an option to switch off.

  Note

  The overestimation can be caused by the error of function approximation(neural network for q table), environment noise, numerical instability and other reasons.

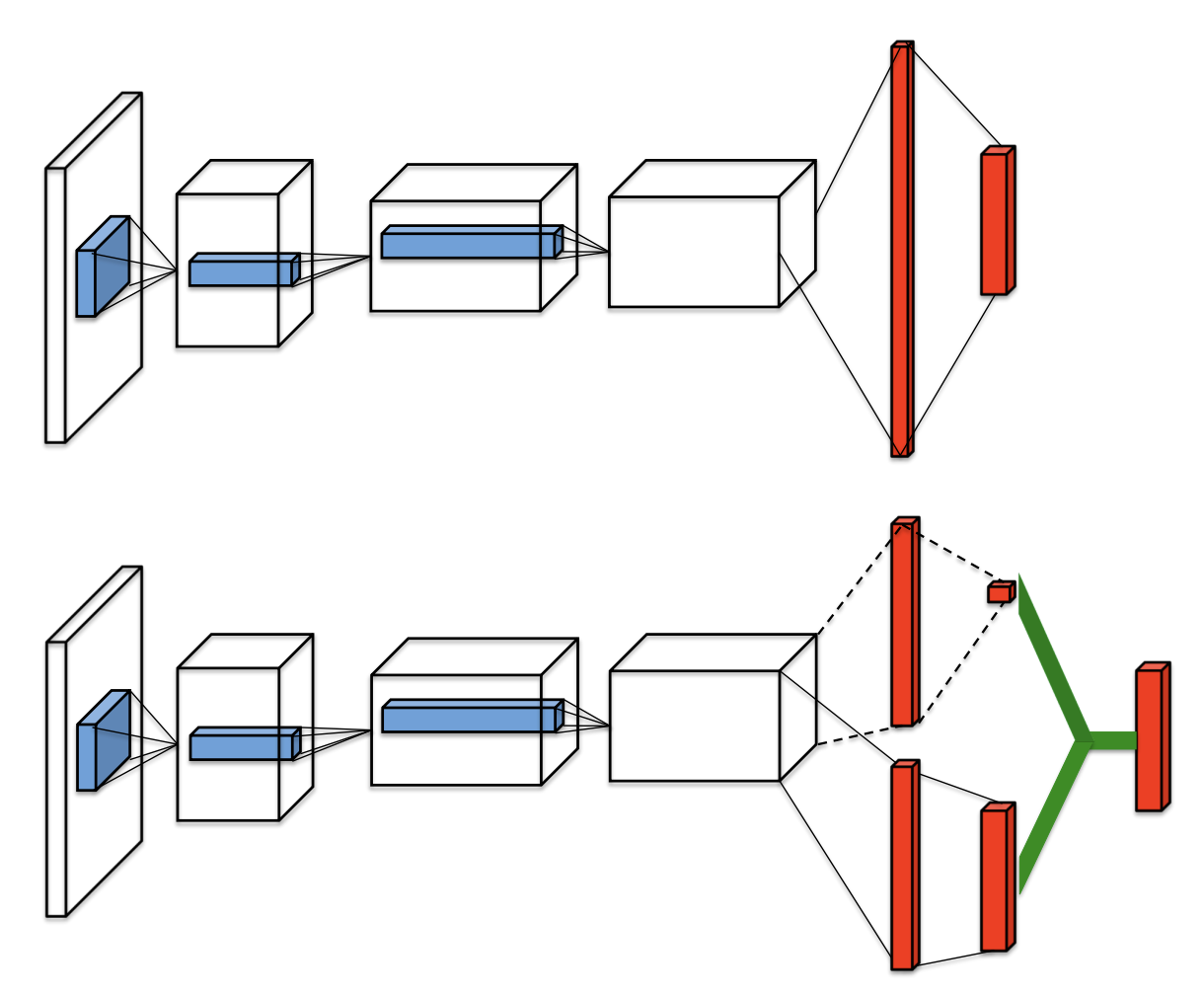
• Dueling head

  In Dueling Network Architectures for Deep Reinforcement Learning, dueling head architecture is utilized to implement the decomposition of state-value and advantage for taking each action, and use these two parts to construct the final q_value, which is better for evaluating the value of some states that show fewer connections with action selection.

  The specific architecture is shown in the following graph:

  

  In DI-engine, users can enable Dueling head by modifying the dueling field in the model part of the configuration file. The detailed code class DuelingHead is located in Dueling Head.

• RNN (DRQN, R2D2)

  For the combination of DQN and RNN, please refer to R2D2 in this series doc.

Implementations

The default config of DQNPolicy is defined as follows:

class ding.policy.dqn.DQNPolicy(cfg: EasyDict, model: Module | None = None, enable_field: List[str] | None = None)

Overview:

Policy class of DQN algorithm, extended by Double DQN/Dueling DQN/PER/multi-step TD.

Config:

ID	Symbol	Type	Default Value	Description	Other(Shape)
1	type	str	dqn	RL policy register name, refer to registry POLICY_REGISTRY	This arg is optional, a placeholder
2	cuda	bool	False	Whether to use cuda for network	This arg can be diff- erent from modes
3	on_policy	bool	False	Whether the RL algorithm is on-policy or off-policy
4	priority	bool	False	Whether use priority(PER)	Priority sample, update priority
5	priority_IS _weight	bool	False	Whether use Importance Sampling Weight to correct biased update. If True, priority must be True.
6	discount_ factor	float	0.97, [0.95, 0.999]	Reward’s future discount factor, aka. gamma	May be 1 when sparse reward env
7	nstep	int	1, [3, 5]	N-step reward discount sum for target q_value estimation
8	model.dueling	bool	True	dueling head architecture
9	model.encoder _hidden _size_list	list (int)	[32, 64, 64, 128]	Sequence of hidden_size of subsequent conv layers and the final dense layer.	default kernel_size is [8, 4, 3] default stride is [4, 2 ,1]
10	model.dropout	float	None	Dropout rate for dropout layers.	[0,1] If set to None means no dropout
11	learn.update per_collect	int	3	How many updates(iterations) to train after collector’s one collection. Only valid in serial training	This args can be vary from envs. Bigger val means more off-policy
12	learn.batch_ size	int	64	The number of samples of an iteration
13	learn.learning _rate	float	0.001	Gradient step length of an iteration.
14	learn.target_ update_freq	int	100	Frequence of target network update.	Hard(assign) update
15	learn.target_ theta	float	0.005	Frequence of target network update. Only one of [target_update_freq, target_theta] should be set	Soft(assign) update
16	learn.ignore_ done	bool	False	Whether ignore done for target value calculation.	Enable it for some fake termination env
17	collect.n_sample	int	[8, 128]	The number of training samples of a call of collector.	It varies from different envs
18	collect.n_episode	int	8	The number of training episodes of a call of collector	only one of [n_sample ,n_episode] should be set
19	collect.unroll _len	int	1	unroll length of an iteration	In RNN, unroll_len>1
20	other.eps.type	str	exp	exploration rate decay type	Support [‘exp’, ‘linear’].
21	other.eps. start	float	0.95	start value of exploration rate	[0,1]
22	other.eps. end	float	0.1	end value of exploration rate	[0,1]
23	other.eps. decay	int	10000	decay length of exploration	greater than 0. set decay=10000 means the exploration rate decay from start value to end value during decay length.

The network interface DQN used is defined as follows:

class ding.model.template.q_learning.DQN(obs_shape: int | SequenceType, action_shape: int | SequenceType, encoder_hidden_size_list: SequenceType = [128, 128, 64], dueling: bool = True, head_hidden_size: int | None = None, head_layer_num: int = 1, activation: Module | None = ReLU(), norm_type: str | None = None, dropout: float | None = None, init_bias: float | None = None)

Overview:

The neural nework structure and computation graph of Deep Q Network (DQN) algorithm, which is the most classic value-based RL algorithm for discrete action. The DQN is composed of two parts: encoder and head. The encoder is used to extract the feature from various observation, and the head is used to compute the Q value of each action dimension.

Interfaces:

__init__, forward.

Note

Current DQN supports two types of encoder: FCEncoder and ConvEncoder, two types of head: DiscreteHead and DuelingHead. You can customize your own encoder or head by inheriting this class.

forward(x: Tensor) → Dict

Overview:

DQN forward computation graph, input observation tensor to predict q_value.

Arguments:

• x (torch.Tensor): The input observation tensor data.

Returns:

• outputs (Dict): The output of DQN’s forward, including q_value.

ReturnsKeys:

• logit (torch.Tensor): Discrete Q-value output of each possible action dimension.

Shapes:

• x (torch.Tensor): \((B, N)\), where B is batch size and N is obs_shape

• logit (torch.Tensor): \((B, M)\), where B is batch size and M is action_shape

Examples:

>>> model = DQN(32, 6)  # arguments: 'obs_shape' and 'action_shape'
>>> inputs = torch.randn(4, 32)
>>> outputs = model(inputs)
>>> assert isinstance(outputs, dict) and outputs['logit'].shape == torch.Size([4, 6])

Note

For consistency and compatibility, we name all the outputs of the network which are related to action selections as logit.

Benchmark

Benchmark and comparison of dqn algorithm

environment	best mean reward	evaluation results	config link	comparison
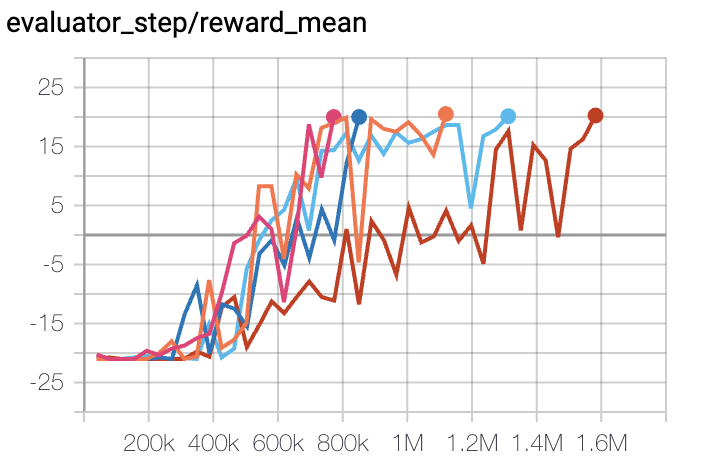
Pong (PongNoFrameskip-v4)	20		config_link_p	Tianshou(20) Sb3(20)
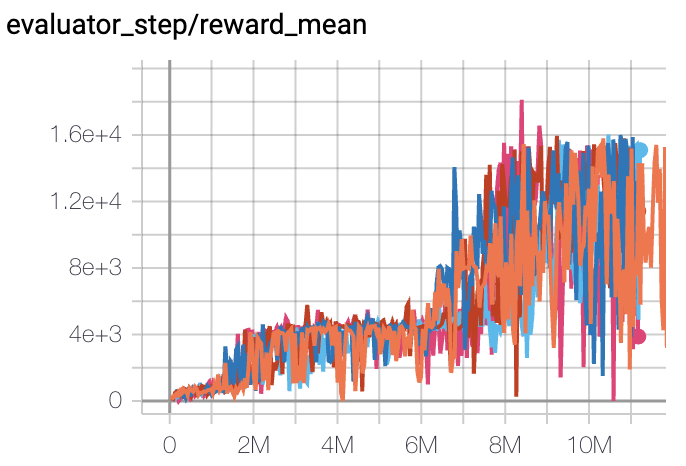
Qbert (QbertNoFrameskip-v4)	17966		config_link_q	Tianshou(7307) Rllib(7968) Sb3(9496)
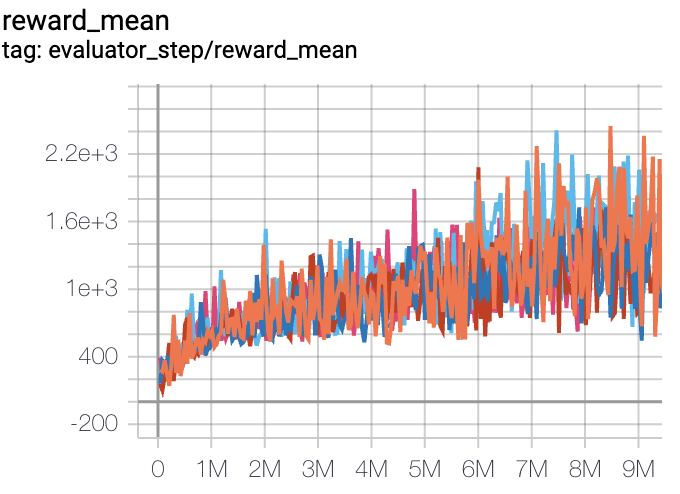
SpaceInvaders (SpaceInvadersNoFrameskip-v4)	2403		config_link_s	Tianshou(812) Rllib(1001) Sb3(622)

P.S.：

1. The above results are obtained by running the same configuration on five different random seeds (0, 1, 2, 3, 4)

2. For the discrete action space algorithm like DQN, the Atari environment set is generally used for testing (including sub-environments Pong), and Atari environment is generally evaluated by the highest mean reward training 10M env_step. For more details about Atari, please refer to Atari Env Tutorial .

Reference

• Mnih, Volodymyr, et al. “Human-level control through deep reinforcement learning.” nature 518.7540 (2015): 529-533.

• Wang, Z., Schaul, T., Hessel, M., Hasselt, H., Lanctot, M., & Freitas, N. (2016, June). Dueling network architectures for deep reinforcement learning. In International conference on machine learning (pp. 1995-2003). PMLR.

• Van Hasselt, H., Guez, A., & Silver, D. (2016, March). Deep reinforcement learning with double q-learning. In Proceedings of the AAAI conference on artificial intelligence (Vol. 30, No. 1).

• Schaul, T., Quan, J., Antonoglou, I., & Silver, D. (2015). Prioritized experience replay. arXiv preprint arXiv:1511.05952.