MDQN¶

Overview¶

MDQN was proposed in Munchausen Reinforcement Learning. They call this general approach “Munchausen Reinforcement Learning” (M-RL), as a reference to a famous passage of The Surprising Adventures of Baron Munchausen by Raspe, where the Baron pulls himself out of a swamp by pulling on his own hair. From a practical point of view, the key difference between MDQN and DQN is that MDQN adding a scaled log-policy to the immediate reward on the Soft-DQN which is is an extension of the traditional DQN algorithm with max entropy.

Quick Facts¶

MDQN is a model-free and value-based RL algorithm.
MDQN only support discrete action spaces.
MDQN is an off-policy algorithm.
MDQN uses eps-greedy for exploration.
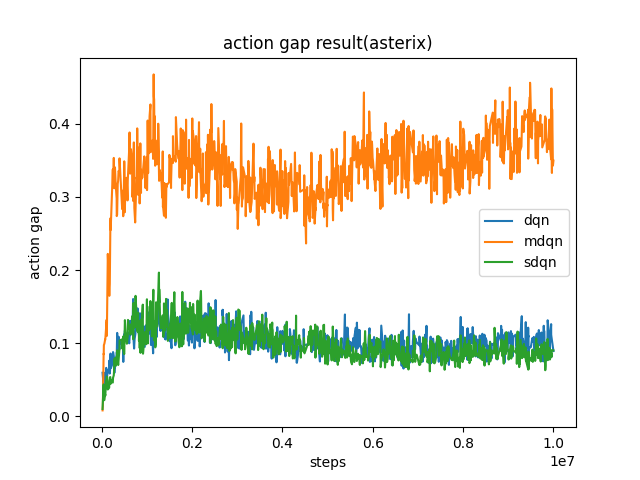
MDQN increased the action gap, and has implicit KL regularization.

Key Equations or Key Graphs¶

The target Q value used in MDQN is:

\[\hat{q}_{\mathrm{m} \text {-dqn }}\left(r_t, s_{t+1}\right)=r_t+\alpha \tau \ln \pi_{\bar{\theta}}\left(a_t \mid s_t\right)+\gamma \sum_{a^{\prime} \in A} \pi_{\bar{\theta}}\left(a^{\prime} \mid s_{t+1}\right)\left(q_{\bar{\theta}}\left(s_{t+1}, a^{\prime}\right)-\tau \ln \pi_{\bar{\theta}}\left(a^{\prime} \mid s_{t+1}\right)\right)\]

For the log-policy \(\alpha \tau \ln \pi_{\bar{\theta}}\left(a_t \mid s_t\right)\) we used the following formula to calculate

\[\tau \ln \pi_{k}=q_k-v_k-\tau \ln \left\langle 1, \exp \frac{q_k-v_k}{\tau}\right\rangle\]

where \(q_k\) is the target_q_current in our code. For the max entropy part \(\tau \ln \pi_{\bar{\theta}}\left(a^{\prime} \mid s_{t+1}\right)\) , we use the same formula to calculate where the where \(q_{k+1}\) is the target_q in our code

And we replace \(\tau \ln \pi(a \mid s)\) by \([\tau \ln \pi(a \mid s)]_{l_0}^0`\) because log-policy term is not bounded, and can cause numerical issues if the policy becomes too close to deterministic.

And we replace \(\pi_{\bar{\theta}}\left(a^{\prime} \mid s_{t+1}\right)\) by \(softmax(q-v)\) which official implementations used but not mentationed in their paper.

And we test action at asterix and get the same result as paper that MDQN could increase the action gap.

Pseudo-code¶

Extension¶

TBD

Implementations¶

The default config of MDQNPolicy is defined as follows:

class ding.policy.mdqn.MDQNPolicy(cfg: EasyDict, model: Module | None = None, enable_field: List[str] | None = None)[source]

Overview:

Policy class of Munchausen DQN algorithm, extended by auxiliary objectives. Paper link: https://arxiv.org/abs/2007.14430.

Config:

ID	Symbol	Type	Default Value	Description	Other(Shape)
1	`type`	str	mdqn	RL policy register name, refer to registry `POLICY_REGISTRY`	This arg is optional, a placeholder
2	`cuda`	bool	False	Whether to use cuda for network	This arg can be diff- erent from modes
3	`on_policy`	bool	False	Whether the RL algorithm is on-policy or off-policy
4	`priority`	bool	False	Whether use priority(PER)	Priority sample, update priority
5	`priority_IS` `_weight`	bool	False	Whether use Importance Sampling Weight to correct biased update. If True, priority must be True.
6	`discount_` `factor`	float	0.97, [0.95, 0.999]	Reward’s future discount factor, aka. gamma	May be 1 when sparse reward env
7	`nstep`	int	1, [3, 5]	N-step reward discount sum for target q_value estimation
8	`learn.update` `per_collect` `_gpu`	int	1	How many updates(iterations) to train after collector’s one collection. Only valid in serial training	This args can be vary from envs. Bigger val means more off-policy
10	`learn.batch_` `size`	int	32	The number of samples of an iteration
11	`learn.learning` `_rate`	float	0.001	Gradient step length of an iteration.
12	`learn.target_` `update_freq`	int	2000	Frequence of target network update.	Hard(assign) update
13	`learn.ignore_` `done`	bool	False	Whether ignore done for target value calculation.	Enable it for some fake termination env
14	`collect.n_sample`	int	4	The number of training samples of a call of collector.	It varies from different envs
15	`collect.unroll` `_len`	int	1	unroll length of an iteration	In RNN, unroll_len>1
16	`other.eps.type`	str	exp	exploration rate decay type	Support [‘exp’, ‘linear’].
17	`other.eps.` `start`	float	0.01	start value of exploration rate	[0,1]
18	`other.eps.` `end`	float	0.001	end value of exploration rate	[0,1]
19	`other.eps.` `decay`	int	250000	decay length of exploration	greater than 0. set decay=250000 means the exploration rate decay from start value to end value during decay length.
20	`entropy_tau`	float	0.003	the ration of entropy in TD loss
21	`alpha`	float	0.9	the ration of Munchausen term to the TD loss

The td error interface MDQN used is defined as follows:

ding.rl_utils.td.m_q_1step_td_error(data: ~collections.namedtuple, gamma: float, tau: float, alpha: float, criterion: <module 'torch.nn.modules' from '/opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages/torch/nn/modules/__init__.py'> = MSELoss()) → Tensor[source]

Overview:

Munchausen td_error for DQN algorithm, support 1 step td error.

Arguments:

data (m_q_1step_td_data): The input data, m_q_1step_td_data to calculate loss
gamma (float): Discount factor
tau (float): Entropy factor for Munchausen DQN
alpha (float): Discount factor for Munchausen term
criterion (torch.nn.modules): Loss function criterion

Returns:

loss (torch.Tensor): 1step td error, 0-dim tensor

Shapes:

data (m_q_1step_td_data): the m_q_1step_td_data containing [‘q’, ‘target_q’, ‘next_q’, ‘act’, ‘reward’, ‘done’, ‘weight’]
q (torch.FloatTensor): \((B, N)\) i.e. [batch_size, action_dim]
target_q (torch.FloatTensor): \((B, N)\) i.e. [batch_size, action_dim]
next_q (torch.FloatTensor): \((B, N)\) i.e. [batch_size, action_dim]
act (torch.LongTensor): \((B, )\)
reward (torch.FloatTensor): \(( , B)\)
done (torch.BoolTensor) \((B, )\), whether done in last timestep
weight (torch.FloatTensor or None): \((B, )\), the training sample weight

Examples:

>>> action_dim = 4
>>> data = m_q_1step_td_data(
>>>     q=torch.randn(3, action_dim),
>>>     target_q=torch.randn(3, action_dim),
>>>     next_q=torch.randn(3, action_dim),
>>>     act=torch.randint(0, action_dim, (3,)),
>>>     reward=torch.randn(3),
>>>     done=torch.randint(0, 2, (3,)),
>>>     weight=torch.ones(3),
>>> )
>>> loss = m_q_1step_td_error(data, 0.99, 0.01, 0.01)

Benchmark¶

Benchmark and comparison of mdqn algorithm¶
environment	best mean reward	config link	comparison
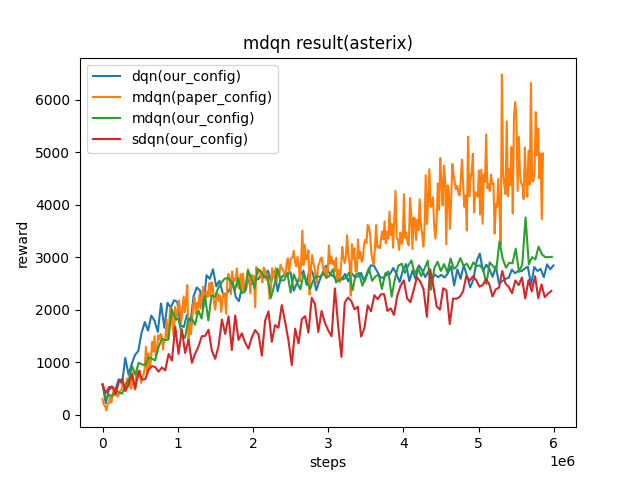
Asterix (Asterix-v0)	8963	config_link_asterix	sdqn(3513) paper(1718) dqn(3444)
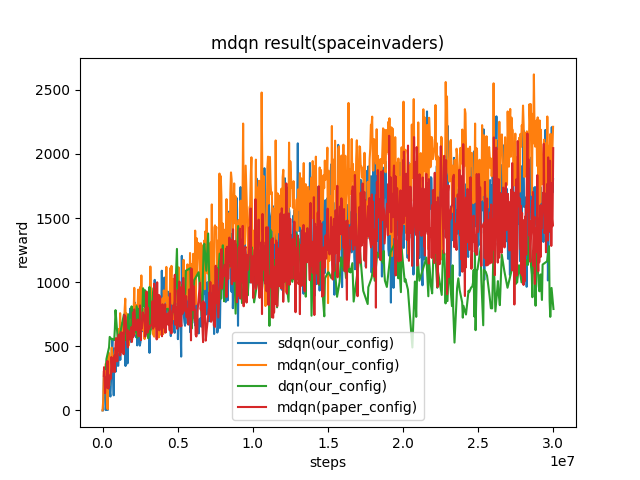
SpaceInvaders (SpaceInvaders-v0)	2211	config_link_spaceinvaders	sdqn(1804) paper(2045) dqn(1228)
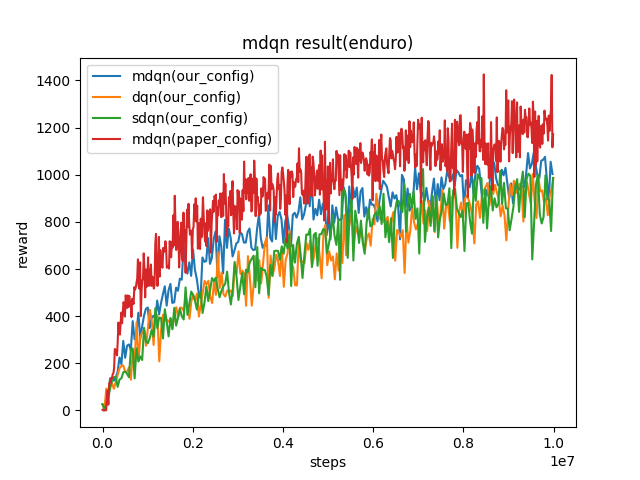
Enduro (Enduro-v4)	1003	config_link_enduro	sdqn(986.1) paper(1171) dqn(986.4)

Key difference between our config and paper config:

we collect 100 samples, train 10 times. In the paper, they collect 4 samples, train 1 time.
we update target network for every 500 iterations, they update target network for every 2000 iterations.
the epsilon we used for exploration is from 1 to 0.05, their epsilon is from 0.01 to 0.001.

P.S.:

The above results are obtained by running the same configuration on seed 0
For the discrete action space algorithm like DQN, the Atari environment set is generally used for testing, and Atari environment is generally evaluated by the highest mean reward training 10M env_step. For more details about Atari, please refer to Atari Env Tutorial .

Reference¶

Vieillard, Nino, Olivier Pietquin, and Matthieu Geist. “Munchausen reinforcement learning.” Advances in Neural Information Processing Systems 33 (2020): 4235-4246.