QMIX

Overview

QMIX is proposed by Rashid et al.(2018) for learning joint action value function conditioned on global state information in multi-agent centralized training, and extracting decentralized policies from the centralized end-to-end framework. QMIX employs a centralized neural network to estimate joint action values as a complex non-linear combination of per-agent action values based on local observations, which provides a novel representation of centralized action-value functions and guarantees consistency between the centralized and decentralized policies.

QMIX is a non-linear extension of VDN (Sunehag et al. 2017). Compared to VDN, QMIX can represent more extra state information during training and a much richer class of action-value functions.

Quick Facts

1. QMIX uses the paradigm of centralized training with decentralized execution.

2. QMIX is a model-free, value-based, off-policy, multi-agent RL method.

3. QMIX only support discrete action spaces.

4. QMIX considers a partially observable scenario in which each agent only obtains individual observations.

5. QMIX accepts DRQN as individual value network to tackle the partially observable issue.

6. QMIX represents the joint value function using an architecture consisting of agent networks, a mixing network, a hyper-network. The mixing network is a feed-forward neural network that takes the agent network outputs as input and mixes them monotonically, producing joint action values. The weights of the mixing network are produced by a separate hypernetwork.

Key Equations or Key Graphs

VDN and QMIX are representative methods that use the idea of factorization of the joint action-value function \(Q_{tot}\) into individual ones \(Q_a\) for decentralized execution.

In order to achieve centralized training with decentralized execution (CTDE), we need to ensure that a global \(argmax\) performed on \(Q_{tot}\) yields the same result as a set of individual \(argmax\) operations performed on each \(Q_a\):

\[\begin{split}$\arg \max _{\boldsymbol{u}} Q_{\mathrm{tot}}(\boldsymbol{\tau}, \boldsymbol{u})=\left(\begin{array}{c}\arg \max _{u_{1}} Q_{1}\left(\tau_{1}, u_{1}\right) \\ \vdots \\ \arg \max _{u_{N}} Q_{N}\left(\tau_{n}, u_{N}\right)\end{array}\right)$\end{split}\]

VDN factorizes the joint action-value function into a sum of individual action-value functions. \($Q_{\mathrm{tot}}(\boldsymbol{\tau}, \boldsymbol{u})=\sum_{i=1}^{N} Q_{i}\left(\tau_{i}, u_{i}\right)$\)

QMIX extends this additive value factorization to represent the joint action-value function as a monotonic function. QMIX is based on monotonicity, a constraint on the relationship between joint action values \(Q_{tot}\) and individual action values \(Q_a\).

\[\frac{\partial Q_{tot}}{\partial Q_{a}} \geq 0， \forall a \in A\]

The overall QMIX architecture including individual agent networks, the mixing network, the hyper-network:

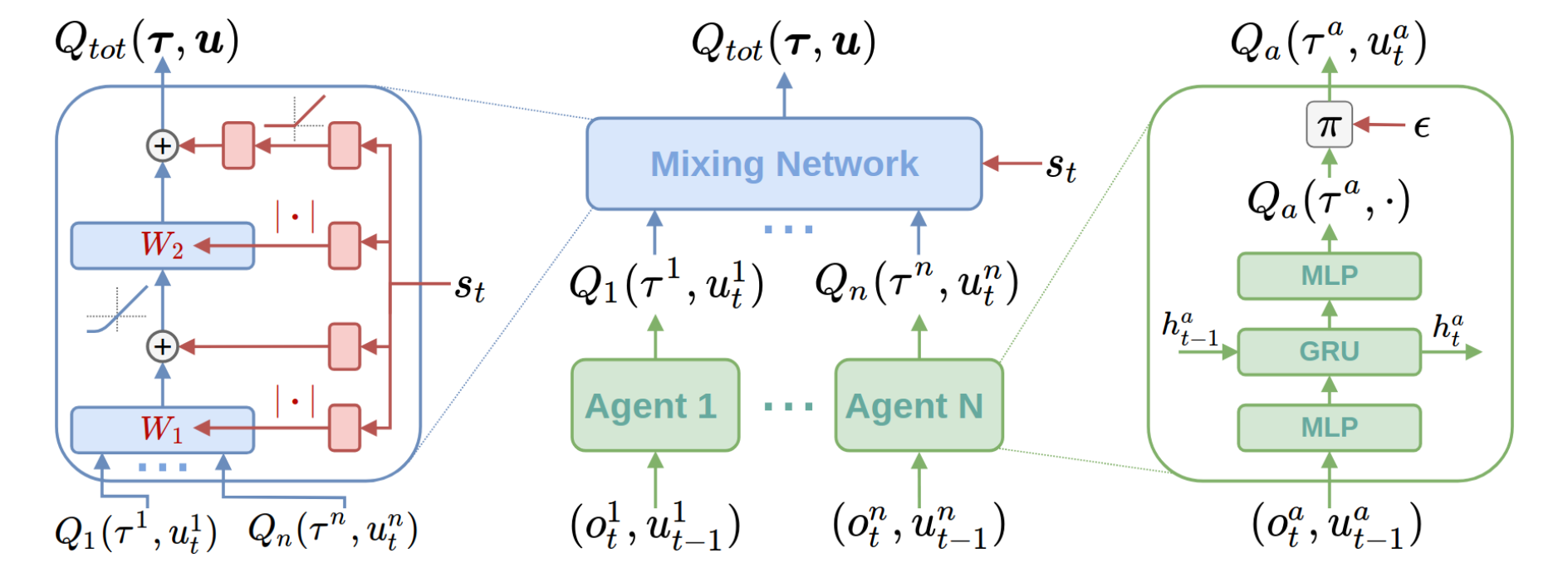
QMIX trains the mixing network via minimizing the following loss:

\[y^{tot} = r + \gamma \max_{\textbf{u}^{’}}Q_{tot}(\tau^{'}, \textbf{u}^{'}, s^{'}; \theta^{-})\]

\[\mathcal{L}(\theta) = \sum_{i=1}^{b} [(y_{i}^{tot} - Q_{tot}(\tau, \textbf{u}, s; \theta)^{2}]\]

Each weight of the mixing network is produced by a independent hyper-network, which takes the global state as input and outputs the weight of one layer of the mixing network. More details can be found in the original paper Rashid et al.(2018).

VDN and QMIX are methods that attempt to factorize \(Q_tot\) assuming additivity and monotonicity, respectively. Thus, joint action value functions satisfying those conditions would be well factorized by VDN and QMIX. However, there exist tasks whose joint action-value functions do not meet the said conditions. QTRAN (Son et al. 2019), proposes a factorization method, which is free from such structural constraints via transforming the original joint action-value function into an easily factorizable one. QTRAN guarantees more general factorization than VDN or QMIX.

Implementations

The default config is defined as follows:

class ding.policy.qmix.QMIXPolicy(cfg: EasyDict, model: Module | None = None, enable_field: List[str] | None = None)

Overview:

Policy class of QMIX algorithm. QMIX is a multi-agent reinforcement learning algorithm, you can view the paper in the following link https://arxiv.org/abs/1803.11485.

Config:

ID	Symbol	Type	Default Value	Description	Other(Shape)
1	type	str	qmix	RL policy register name, refer to registry POLICY_REGISTRY	this arg is optional, a placeholder
2	cuda	bool	True	Whether to use cuda for network	this arg can be diff- erent from modes
3	on_policy	bool	False	Whether the RL algorithm is on-policy or off-policy
	priority	bool	False	Whether use priority(PER)	priority sample, update priority
5	priority_ IS_weight	bool	False	Whether use Importance Sampling Weight to correct biased update.	IS weight
6	learn.update_ per_collect	int	20	How many updates(iterations) to train after collector’s one collection. Only valid in serial training	this args can be vary from envs. Bigger val means more off-policy
7	learn.target_ update_theta	float	0.001	Target network update momentum parameter.	between[0,1]
8	learn.discount _factor	float	0.99	Reward’s future discount factor, aka. gamma	may be 1 when sparse reward env

The network interface QMIX used is defined as follows:

class ding.model.template.QMix(agent_num: int, obs_shape: int, global_obs_shape: int | List[int], action_shape: int, hidden_size_list: list, mixer: bool = True, lstm_type: str = 'gru', activation: Module = ReLU(), dueling: bool = False)

Overview:

The neural network and computation graph of algorithms related to QMIX(https://arxiv.org/abs/1803.11485). The QMIX is composed of two parts: agent Q network and mixer(optional). The QMIX paper mentions that all agents share local Q network parameters, so only one Q network is initialized here. Then use summation or Mixer network to process the local Q according to the mixer settings to obtain the global Q.

Interface:

__init__, forward.

forward(data: dict, single_step: bool = True) → dict

Overview:

QMIX forward computation graph, input dict including time series observation and related data to predict total q_value and each agent q_value.

Arguments:

• data (dict): Input data dict with keys [‘obs’, ‘prev_state’, ‘action’].

  • agent_state (torch.Tensor): Time series local observation data of each agents.

  • global_state (torch.Tensor): Time series global observation data.

  • prev_state (list): Previous rnn state for q_network.

  • action (torch.Tensor or None): The actions of each agent given outside the function. If action is None, use argmax q_value index as action to calculate agent_q_act.

• single_step (bool): Whether single_step forward, if so, add timestep dim before forward and remove it after forward.

Returns:

• ret (dict): Output data dict with keys [total_q, logit, next_state].

ReturnsKeys:

• total_q (torch.Tensor): Total q_value, which is the result of mixer network.

• agent_q (torch.Tensor): Each agent q_value.

• next_state (list): Next rnn state for q_network.

Shapes:

• agent_state (torch.Tensor): \((T, B, A, N)\), where T is timestep, B is batch_size A is agent_num, N is obs_shape.

• global_state (torch.Tensor): \((T, B, M)\), where M is global_obs_shape.

• prev_state (list): math:(B, A), a list of length B, and each element is a list of length A.

• action (torch.Tensor): \((T, B, A)\).

• total_q (torch.Tensor): \((T, B)\).

• agent_q (torch.Tensor): \((T, B, A, P)\), where P is action_shape.

• next_state (list): math:(B, A), a list of length B, and each element is a list of length A.

Benchmark

Benchmark and comparison of qmix algorithm

environment	best mean reward	evaluation results	config link	comparison
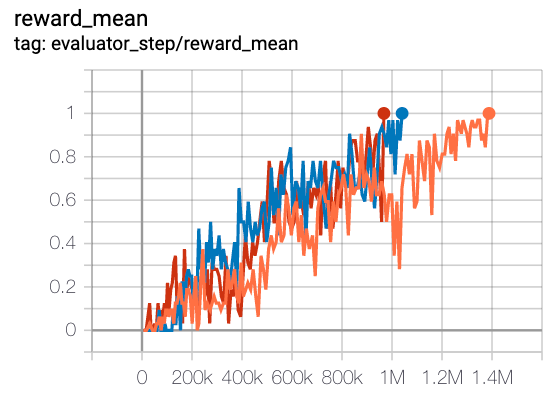
MMM	1		config_link_MMM	Pymarl(1)
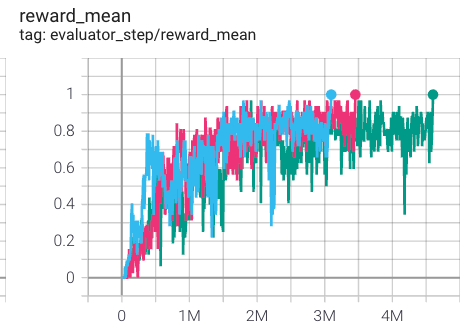
3s5z	1		config_link_3s5z	Pymarl(1)
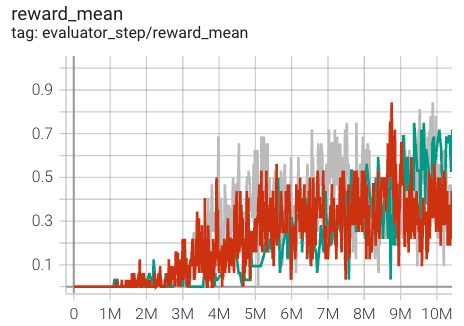
MMM2	0.8		config_link_MMM2	Pymarl(0.7)
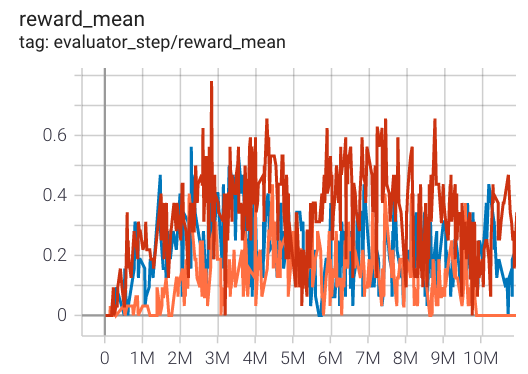
5m6m	0.6		config_link_5m6m	Pymarl(0.76)
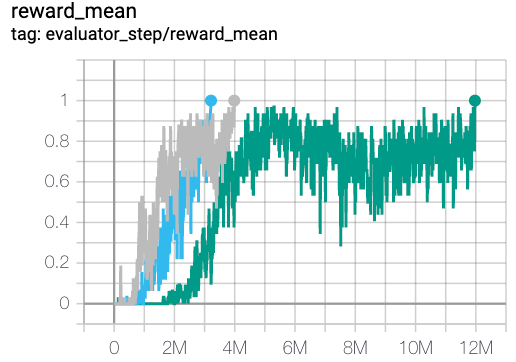
2c_vs_64zg	1		config_link_2c_vs_64zg	Pymarl(1)

P.S.：

1. The above results are obtained by running the same configuration on five different random seeds (0, 1, 2).

2. For the multi-agent discrete action space algorithm like QMIX, the SMAC environment set is generally used for testing, and is generally evaluated by the highest mean reward training 10M env_step. For more details about SMAC, please refer to SMAC Env Tutorial .

References

• Tabish Rashid, Mikayel Samvelyan, Christian Schroeder de Witt, Gregory Farquhar, Jakob Foerster, Shimon Whiteson. Qmix: Monotonic value function factorisation for deep multi-agent reinforcement learning. International Conference on Machine Learning. PMLR, 2018.

• Peter Sunehag, Guy Lever, Audrunas Gruslys, Wojciech Marian Czarnecki, Vinicius Zambaldi, Max Jaderberg, Marc Lanctot, Nicolas Sonnerat, Joel Z. Leibo, Karl Tuyls, Thore Graepel. Value-decomposition networks for cooperative multi-agent learning. arXiv preprint arXiv:1706.05296, 2017.

• Kyunghwan Son, Daewoo Kim, Wan Ju Kang, David Earl Hostallero, Yung Yi. QTRAN: Learning to Factorize with Transformation for Cooperative Multi-Agent Reinforcement Learning. International Conference on Machine Learning. PMLR, 2019.

• Mikayel Samvelyan, Tabish Rashid, Christian Schroeder de Witt, Gregory Farquhar, Nantas Nardelli, Tim G. J. Rudner, Chia-Man Hung, Philip H. S. Torr, Jakob Foerster, Shimon Whiteson. The StarCraft Multi-Agent Challenge. arXiv preprint arXiv:1902.04043, 2019.

Other Public Implementations

• pymarl