Table of Contents
Shortcuts

QRDQN

Overview

QR (Quantile Regression) DQN was proposed in Distributional Reinforcement Learning with Quantile Regression and inherits the idea of learning the distribution of a q-value. Instead of approximate the distribution density function with discrete atoms, QRDQN, directly regresses a discrete set of quantiles of a q-value.

Quick Facts

  1. QRDQN is a model-free and value-based RL algorithm.

  2. QRDQN only support discrete action spaces.

  3. QRDQN is an off-policy algorithm.

  4. Usually, QRDQN use eps-greedy or multinomial sample for exploration.

  5. QRDQN can be equipped with RNN.

Key Equations or Key Graphs

C51 uses N fixed locations for its approximation distribution and adjusts their probabilities, while QRDQN assigns fixed, uniform probabilities to N adjustable locations. Based on this, QRDQN uses quantile regression to stochastically adjust the distributions’ locations so as to minimize the Wasserstein distance to a target distribution.

The quantile regression loss, for a quantile \(\tau \in [0, 1]\), is an asymmetric convex loss function that penalizes overestimation errors with weight \(\tau\) and underestimation errors with weight \(1−\tau\). For a distribution \(Z\), and a given quantile \(\tau\), the value of the quantile function \(F_Z^{−1}(\tau)\) may be characterized as the minimizer of the quantile regression loss:

\[\begin{split}\begin{array}{r} \mathcal{L}_{\mathrm{QR}}^{\tau}(\theta):=\mathbb{E}_{\hat{z} \sim Z}\left[\rho_{\tau}(\hat{Z}-\theta)\right], \text { where } \\ \rho_{\tau}(u)=u\left(\tau-\delta_{\{u<0\}}\right), \forall u \in \mathbb{R} \end{array}\end{split}\]

And the above mentioned loss is not smooth at zero, which can limit performance when using non-linear function approximation. Therefore, a modified quantile loss, called quantile huber loss is applied during the Bellman update of QRDQN (i.e. the equation 10 in the following pseudo-code).

\[\rho^{\kappa}_{\tau}(u)=L_{\kappa}(u)\lvert \tau-\delta_{\{u<0\}} \rvert\]

Where \(L_{\kappa}\) is Huber Loss.

Note

Compared with DQN, QRDQN has these differences:

  1. Neural network architecture, the output layer of QRDQN is of size M x N, where M is the size of discrete action space and N is a hyper-parameter giving the number of quantile targets.

  2. Replace DQN loss with the quantile huber loss.

  3. In original QRDQN paper, replace RMSProp optimizer with Adam. While in DI-engine, we always use Adam optimizer.

Pseudo-code

../_images/QRDQN.png

Extensions

QRDQN can be combined with:

  • PER (Prioritized Experience Replay)

  • Multi-step TD-loss

  • Double (target) network

  • RNN

Implementation

Tip

Our benchmark result of QRDQN uses the same hyper-parameters as DQN except the QRDQN’s exclusive hyper-parameter, the number of quantiles, which is empirically set as 32.

The default config of QRDQN is defined as follows:

class ding.policy.qrdqn.QRDQNPolicy(cfg: EasyDict, model: Module | None = None, enable_field: List[str] | None = None)[source]
Overview:

Policy class of QRDQN algorithm. QRDQN (https://arxiv.org/pdf/1710.10044.pdf) is a distributional RL algorithm, which is an extension of DQN. The main idea of QRDQN is to use quantile regression to estimate the quantile of the distribution of the return value, and then use the quantile to calculate the quantile loss.

Config:

ID

Symbol

Type

Default Value

Description

Other(Shape)

1

type

str

qrdqn
RL policy register name, refer to
registry POLICY_REGISTRY
this arg is optional,
a placeholder

2

cuda

bool

False
Whether to use cuda for network
this arg can be diff-
erent from modes

3

on_policy

bool

False
Whether the RL algorithm is on-policy
or off-policy

4

priority

bool

True
Whether use priority(PER)
priority sample,
update priority

6
other.eps
.start

float

0.05
Start value for epsilon decay. It’s
small because rainbow use noisy net.

7
other.eps
.end

float

0.05
End value for epsilon decay.

8
discount_
factor

float

0.97, [0.95, 0.999]
Reward’s future discount factor, aka.
gamma
may be 1 when sparse
reward env

9

nstep

int

3, [3, 5]
N-step reward discount sum for target
q_value estimation

10
learn.update
per_collect

int

3
How many updates(iterations) to train
after collector’s one collection. Only
valid in serial training
this args can be vary
from envs. Bigger val
means more off-policy

11

learn.kappa

float

/
Threshold of Huber loss

The network interface QRDQN used is defined as follows:

class ding.model.template.q_learning.QRDQN(obs_shape: int | SequenceType, action_shape: int | SequenceType, encoder_hidden_size_list: SequenceType = [128, 128, 64], head_hidden_size: int | None = None, head_layer_num: int = 1, num_quantiles: int = 32, activation: Module | None = ReLU(), norm_type: str | None = None)[source]
Overview:

The neural network structure and computation graph of QRDQN, which combines distributional RL and DQN. You can refer to Distributional Reinforcement Learning with Quantile Regression https://arxiv.org/pdf/1710.10044.pdf for more details.

Interfaces:

__init__, forward

forward(x: Tensor) → Dict[source]
Overview:

Use observation tensor to predict QRDQN’s output. Parameter updates with QRDQN’s MLPs forward setup.

Arguments:
  • x (torch.Tensor):

    The encoded embedding tensor with (B, N=hidden_size).

Returns:
  • outputs (Dict):

    Run with encoder and head. Return the result prediction dictionary.

ReturnsKeys:

  • logit (torch.Tensor): Logit tensor with same size as input x.

  • q (torch.Tensor): Q valye tensor tensor of size (B, N, num_quantiles)

  • tau (torch.Tensor): tau tensor of size (B, N, 1)

Shapes:

  • x (torch.Tensor): \((B, N)\), where B is batch size and N is head_hidden_size.

  • logit (torch.FloatTensor): \((B, M)\), where M is action_shape.

  • tau (torch.Tensor): \((B, M, 1)\)

Examples:
>>> model = QRDQN(64, 64)
>>> inputs = torch.randn(4, 64)
>>> outputs = model(inputs)
>>> assert isinstance(outputs, dict)
>>> assert outputs['logit'].shape == torch.Size([4, 64])
>>> # default num_quantiles : int = 32
>>> assert outputs['q'].shape == torch.Size([4, 64, 32])
>>> assert outputs['tau'].shape == torch.Size([4, 32, 1])

The bellman updates of QRDQN is implemented in the function qrdqn_nstep_td_error of ding/rl_utils/td.py.

Benchmark

Benchmark and comparison of QRDQN algorithm

environment

best mean reward

evaluation results

config link

comparison
Pong
(PongNoFrameskip-v4)

20

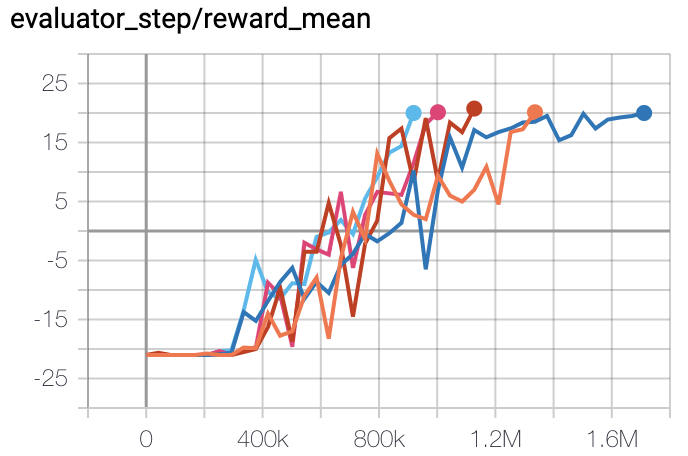
 ../_images/qrdqn_pong.png

config_link_p
Tianshou (20)
Qbert
(QbertNoFrameskip-v4)

18306

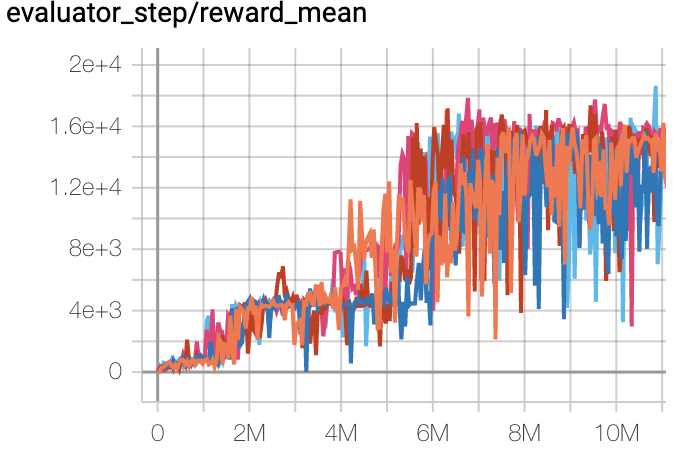
 ../_images/qrdqn_qbert.png

config_link_q
Tianshou (14990)
SpaceInvaders
(SpaceInvadersNoFrame skip-v4)

2231

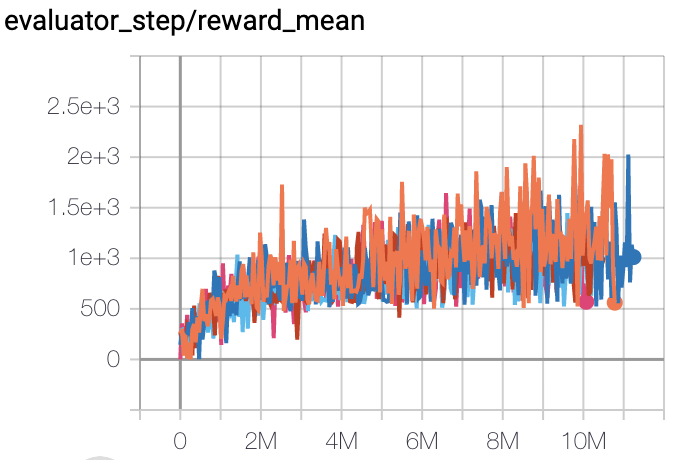
 ../_images/qrdqn_spaceinvaders.png

config_link_s
Tianshou (938)

P.S.：

  1. The above results are obtained by running the same configuration on five different random seeds (0, 1, 2, 3, 4)

  2. For the discrete action space algorithm like QRDQN, the Atari environment set is generally used for testing (including sub-environments Pong), and Atari environment is generally evaluated by the highest mean reward training 10M env_step. For more details about Atari, please refer to Atari Env Tutorial .

References

(QRDQN) Will Dabney, Mark Rowland, Marc G. Bellemare, Rémi Munos: “Distributional Reinforcement Learning with Quantile Regression”, 2017; arXiv:1710.10044. https://arxiv.org/pdf/1710.10044

Other Public Implementations