Table of Contents
Shortcuts

强化学习中的探索机制

本文主要参考这篇关于强化学习中探索策略的综述博客[14] 。

问题定义和研究动机

强化学习，是通过环境给出的奖励信号来指导策略的更新，力求获取最大累计折扣奖励。但在很多现实世界环境中奖励是稀疏的，甚至完全没有奖励。如何在这种情况下，引导智能体高效地探索状态和动作空间，进而找到最优策略完成任务？

因为如果智能体在有限步的训练之后变得贪婪，即在某个状态下只选择当前它认为最优的动作，它可能永远学不到最优策略，因为它很可能已经收敛到了次优策略，永远到达不了真正有意义的奖励大的状态。这即是所谓的探索与利用困境问题。 通俗来讲，所谓探索：是指做你以前从来没有做过的事情，以期望获得更高的回报；所谓利用：是指做你当前知道的能产生最大回报的事情。

参考 Go-Explore [9]，探索困难的问题主要包括两个难点：

  • 环境给出的奖励很稀疏。智能体需要作出特定的序列动作才可能得到一个非零的奖励，如果每一步仅仅采用随机探索，很可能在整个学习过程中都遇不到一个非零的奖励。例如在 Montezuma’s Revenge 里面智能体需要执行长序列动作，才能获取钥匙或者进入新的房间，这时才会有一个奖励。

  • 环境给出的奖励具有误导性。例如在 Pitfall 游戏里面，不仅奖励很稀疏，而且智能体的很多动作会得到一个负的奖励，智能体在学习到如何获取一个正的奖励之前，可能会由于这些负的奖励的存在，停在原地不动，导致缺乏探索。

在上述情况下，一个高效的探索机制对于智能体完成任务至关重要。

研究方向

强化学习中的探索机制可以大致分为以下几个研究方向：

  1. 经典的探索机制

  2. 基于内在奖励的探索

    • 基于计数的内在奖励

    • 基于预测误差的内在奖励

    • 基于信息论的内在奖励

  3. 基于 Memory 的探索

    • Episodic Memory

    • 直接探索

  4. 其他探索机制

各个研究方向的代表性算法及其关键要点，请参见下图：

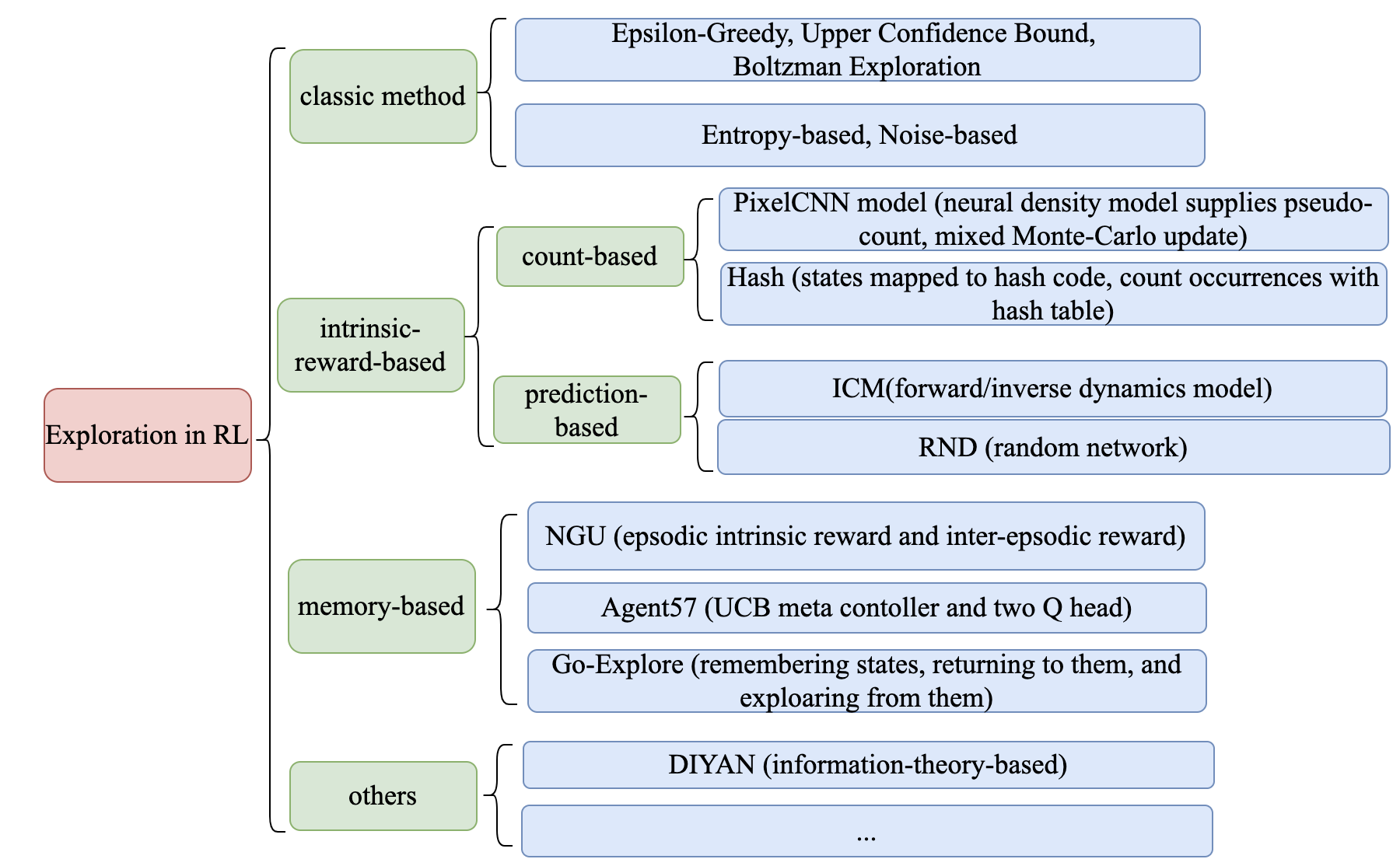
../_images/exploration_overview.png

经典的探索机制

在传统的 multi-armed bandit 问题中，常用的经典探索机制包括：

  • Epsilon-Greedy：在某一时刻，所有动作的选择概率都大于0。智能体以一个较小的概率\(\epsilon\)执行随机的动作（探索），以一个较大的概率\(1-\epsilon\)执行Q值最大的动作（利用）。

  • Upper Confidence Bounds：智能体贪婪地选取最大化置信上界\(\hat{Q}_{t}(a)+\hat{U}_{t}(a)\)的动作，其中\(\hat{Q}_{t}(a)\)是在 \(t\) 时刻前与动作 \(a\)有关的平均奖励，\(\hat{U}_{t}(a)\) 是一个与采取动作 \(a\) 的次数成反比的函数。

  • Boltzmann Exploration：智能体从学习到的 Q 值对应的玻尔兹曼分布 (即对Q值 的 logits 执行 softmax 操作后得到的分布) 中采样动作，可以通过温度参数调整探索程度。

当通过神经网络进行函数近似时，以下机制可用于在深度强化学习训练中得到更好的探索效果：

  • Entropy Loss：通过在损失函数上增加额外的熵正则化项，来鼓励智能体执行更多样化的动作。

  • Noise-based Exploration：通过在观察、动作甚至网络的参数空间添加噪声来实现探索。

基于内在奖励的探索

探索机制设计中比较重要的一类方法就是设计特殊的 reward，从而激发智能体的“好奇心”。一般地，我们将环境给出的奖励称为外在奖励（extrinsic reward)，而探索机制给出的奖励称为内在奖励（intrinsic reward)。

我们希望通过增加这个额外的内在奖励来实现下列两种目的：

  1. 对状态空间的探索：激励智能体探索更多的新颖状态 (novel state)。(需要评估状态\(s\)的新颖性)

  2. 对状态动作空间的探索：激励智能体执行有利于减少对于环境不确定性的动作。(需要评估状态动作对 \((s,a)\) 的新颖性)

首先定性地给出新颖性的定义：

  • 对于某个状态\(s\)，在智能体之前访问过的所有状态中，如果与\(s\)类似的状态数量越少，我们就称状态\(s\)越新颖 (状态动作对 \((s,a)\) 的新颖性的定义与此类似)。

某个状态\(s\)越新颖，通常对应智能体对状态\(s\)的认知不够充分，需要智能体在之后与环境交互时，更多地探索这个状态\(s\)的邻近区域， 因此，这种特别设计的探索机制就会赋予该状态更大的内在奖励。那状态\(s\)的新颖性具体如何度量呢？主要有2种方式，一是通过某种方式对状态进行计数来衡量，二是基于某个预测问题的预测误差来衡量， 这样就分别得到了基于内在奖励的探索下面的2大子类算法：基于计数的内在奖励和基于预测误差的内在奖励。

基于计数的内在奖励

基于计数的内在奖励采用最简单的思想，即通过计数度量新颖性，即每个 \(s\) 都对应一个访问计数\(N(s)\)，其值越大，说明之前智能体对其访问的次数越多，也即对 \(s\) 探索的越充分 (或者说 \(s\) 越不新颖)。探索模块给出一个与状态计数成反比的内在奖励。

但基于计数的方法度量新颖性存在很多明显的局限性：

  • 高维连续观测空间和连续动作空间没有简单的计数方法。

  • 访问计数不能准确地度量智能体对 \((s,a)\) 的认知程度。

基于预测误差的内在奖励

基于预测误差的内在奖励是利用状态在某个预测问题 (通常是监督学习问题) 上的预测误差来度量新颖性。根据在监督学习中神经网络拟合数据集的特性，如果智能体在某个状态\(s\)上预测误差越大，近似说明在状态\(s\) 附近的状态空间上智能体之前访问的次数少，从而该状态\(s\) 新颖性较大。

预测问题往往是与环境的 dynamics 相关的问题，例如论文 [3] Curiosity-driven Exploration by Self-supervised Prediction (ICM) 提出了一种新的基于预测误差的内在好奇心模块 (Intrinsic Curiosity Module，ICM)，通过在原始问题空间上，利用逆向动力学模型和前向动力学模型来学习一个新的特征空间，促使学习到的特征空间只编码影响智能体决策的部分，而忽视掉环境中的噪声等无关干扰。然后在这个更纯粹的特征空间上，根据前向模型预测误差来为 RL 训练提供 intrinsic reward。关于 ICM 的更多细节可以参考博客。

但是 ICM 存在如下问题：

  • 在大规模问题上，环境的前向动力学模型很复杂，加上神经网络容量有限，导致在状态动作空间的某些区域访问次数很大时，预测误差仍然可能很大。

  • 在有些环境上，环境的状态转移函数是随机函数，例如包含 noisy-TV 属性的环境 ，智能体不可能通过通常的神经网络准确预测的下一状态。

为了缓解上述问题，论文 [4] Exploration by Random Network Distillation一文提出 RND 算法，它也是一种基于预测问题的探索方法，不过特殊的是，RND 算法中的预测问题是只和观测状态 (observation) 相关的随机蒸馏问题，不是关于环境的前向或逆向动力学模型。具体地，RND 利用2个结构相同的神经网络：一个固定随机初始化参数的目标网络 (target network)。一个预测器网络 (predictor network)，预测器网络用于输出对目标网络给出的状态编码的预测值。然后 RND 内在探索奖励定义为正比于预测器网络预测的状态特征\(\hat{f}(s_t)\)与目标网络的状态特征\(f(s_t)\)之间的误差。关于 RND 的更多细节可以参考博客。

基于信息论的内在奖励

为了鼓励探索, 另一个思路是设计基于信息理论的内在奖励。 论文 [11] 引入了变分信息最大化探索 (Variational information maximizing exploration, VIME)，核心思想在于最大化智能体对环境动力学信念的信息增益 (maximization of information gain about the agent’s belief of environment dynamics)，在贝叶斯神经网络中使用变分推理，它可以有效地处理连续的状态和动作空间。 论文 [12] 提出 EMI 算法 (Exploration with Mutual Information)，不是通过通常的编解码原始状态或动作空间来学习表征，而是通过最大化相关状态动作表征之间的互信息来学习状态和动作的表征， 他们在实验中验证了在这样的表征空间中提取到的前向预测信号可以很好地指导探索。 此外还有基于互信息的目标函数学习 skill 变量的 DIYAN [13] 等方法，可以在没有外在奖励的条件下，通过设置互信息相关的内在奖励，自动学习到状态与 skill 的分布，用于后续的分层学习，模仿学习和探索等任务中。

基于 Memory 的探索

ICM, RND 等基于内在奖励的探索方法提出通过预测问题的误差来度量状态的新颖性，为新颖性大的状态提供一个大的内在奖励，促进探索，这些方法在许多稀疏奖励设置下，探索困难的任务上取得了不错的效果，但是存在一个问题：随着智能体训练步数的增加，预测问题的预测误差开始减小，探索信号变小，即不再鼓励智能体再次访问某些状态，但是有可能这些状态正是获得外在奖励所必须访问的状态。而且还可能存在以下问题：

  • 函数逼近速度比较慢，有时跟不上智能体探索的速度，导致内在奖励不能很好描述状态的新颖性。

  • 探索的奖励是非平稳的。

基于存储的探索的探索机制，显式利用一个 Memory 维护历史的状态，然后根据当前状态与历史状态的某中度量给出当前状态的内在奖励值。

Episodic Memory

NGU

为了解决前述探索信号逐渐衰减的问题，论文 [5] Never Give Up: Learning Directed Exploration Strategies基于 R2D2 [6] 算法提出了 Never Give Up（NGU）算法。 这种智能体采用一种新的内在奖励产生机制，融合了2个维度的新颖性：即life-long 维度上的局间内在奖励和单局维度上的局内内在奖励，此外还提出通过同时学习一组具有不同探索程度的策略 (directed exploratory policies)来采集更为丰富的样本用于训练。其中局间内在奖励是通过维护一个存储本局状态的 Episodic Memory, 计算当前状态与 Memory 中与其最相似的k个样本的距离计算得到的。关于 NGU 的更多细节可以参考 NGU 中文博客 。

Agent57

论文 [7] Agent57: Outperforming the Atari Human Benchmark在 NGU 的基础上做了如下改进：

  • Q 函数的参数化方式：将 Q 网络分为2部分，分别学习内在奖励对应的 Q 值和外在奖励对应的Q值。

  • NGU 是等概率地使用不同的 Q function (也可以称为策略)，通过 meta-controller 去自适应地选择对应不同奖励折扣因子和内在奖励权重系数的 Q 函数，以平衡探索与利用。

  • 最后使用了更大的 Backprop Through Time Window Size。

直接探索

Go-Explore

Go-Explore [8] [9] 指出当前阻碍智能体探索的因素有2个：忘记了如何到达之前访问过的状态 (detachment)；智能体无法首先返回某个状态，然后从那个状态上开始探索(derailment)。为此作者提出记住状态，返回那个状态，从那个状态开始探索的简单机制，用于应对上述问题：通过维护一个感兴趣状态的存储器以及如何通向这些状态的轨迹，智能体可以回到 (假设模拟器是确定性的) 这些有希望的状态，并从那里继续进行随机探索。

具体地，首先状态被映射成一个短的离散编码（称为 cell ）以便存储。如果出现新的状态或找到更好/更短的轨迹，存储器就会更新相应的状态和轨迹。智能体可以在存储器中均匀随机选择一个状态返回，或者根据某种启发式规则，例如可以根据新旧程度，访问计数，在存储器中它的邻居计数等相关指标选择返回的状态。然后在这个状态上开始探索。Go-Explore 重复上述过程，直到任务被解决，即至少找到一条成功的轨迹。

其他探索机制

除了上述探索机制外，还有基于 Q 值的探索 [10] 等等，感兴趣的读者，可以参考这篇关于强化学习中的探索策略的综述博客[14] 。

未来展望

  • 目前基于内在奖励的探索方法中，如何自适应设置内在奖励和环境给出奖励的相对权重是一个值得研究的问题。

  • 可以观察到目前已有的探索机制，往往是考虑单个状态的新颖性，未来或许可以拓展到序列状态的新颖性，以实现更高语义层面的探索。

  • 目前基于内在奖励的探索和基于 Memory 的探索只是在实践上给出了不错的结果，其理论上的收敛性和最优性还有待研究。

  • 如何将传统探索方法，例如 UCB 与最新的基于内在奖励或基于 Memory 的探索机制相结合或许是一个值得研究的问题。

参考文献