基本概念¶
强化学习 (reinforcement learning,RL) 主要专注于智能体(agent)如何选择最优动作以最大化环境(environment)给出的累计折扣奖励/回报(cumulated discounted reward/return)。首先简单描述智能体与环境交互 (interaction) 的过程,智能体从环境中接收观察到的状态 (state/observation),然后根据接收到的状态选择动作 (action),这个动作会在环境之中被执行,环境会根据智能体采取的动作,转移到下一个状态并给予智能体动作的反馈奖励 (reward)。这个过程循环发生,智能体/强化学习的目标是学会一种最优策略 (policy), 能够最大化积累智能体接收到的奖励。
我们首先形式化定义以下强化学习的基础概念:
Markov Decision Processes
State and Action Spaces
Reward and Return
Policy
然后会进一步解释以下强化学习的方法概念:
Value Function
Policy Gradients
Actor Critic
Model-based RL
最后还回答了一些强化学习领域中常见的概念性问题,以供参考。
马尔可夫决策过程/MDP¶
在强化学习领域,我们通过将智能体与环境交互的过程建模为一个马尔可夫决策过程 (Markov Decision Processes, MDP) ,可以说马尔可夫决策过程是强化学习的基本框架。
马尔可夫性质(Markov property)是指一个随机过程在给定当前时刻状态及所有过去时刻状态情况下,其下一时刻状态的条件概率分布仅依赖于当前时刻状态。即 \(p\left(s_{t+1} \mid s_{t}\right)=p\left(s_{t+1} \mid h_{t}\right) =p(s_{t+1} \mid (s_{1}, s_{2}, s_{3}, \ldots, s_{t})\).
若随机变量序列中的每个状态都满足马尔科夫性质,则称此随机过程为马尔科夫过程。马尔科夫过程通常用一个二元组 \((S,P)\) 来表示,且满足: \(S\)是状态集合,\(P\)是状态转移概率。马尔科夫过程中不存在动作和奖励。将动作和奖励考虑在内的马尔科夫过程称为马尔科夫决策过程。
马尔科夫决策过程由五元组 \((S,A,P,R,\gamma)\) 定义, 其中\(S\)为状态集和,\(A\)为动作集和, \(P\)为状态转移函数, \(R\)为奖励函数, \(\gamma \in [0,1)\)为折扣因子, 定义了问题的horizon。跟马尔科夫过程不同的是,马尔科夫决策过程的状态转移概率为\(P\left(s_{t+1} \mid s_{t}, a_{t}\right)\)。为了数学上的方便,我们通常假设 \(S\) 和\(A\)是有限的集合。
通常我们将智能体与环境交互形成的(状态,动作,奖励)序列,称为轨迹, 记为\(\tau_t=(s_0,a_0,r_0, s_1,...,s_t,a_t,r_t)\)。
强化学习的目标是给定一个马尔科夫决策过程,寻找最优策略\(\pi^*\)。其中策略 \(\pi(a|s)\) 是状态到动作的映射,通常是一个随机概率分布函数,定义了在每个状态\(s\)上执行动作\(a\)的概率。
状态空间/State Spaces¶
状态 state,一般用\(s\)表示,是对环境的全局性描述,观测 observation 一般用\(o\)表示,是对环境的局部性描述。一般环境会使用实值向量、矩阵或高阶张量来表示状态和观察的结果。例如,Atari 游戏中使用 RGB 图片来表示游戏环境的信息,MuJoCo 控制任务中使用向量来表示智能体的状态。
当智能体能够接收到环境全部的状态信息\(s\) 时,我们称环境为完全可观测的 (fully observable),当智能体只能接收部分环境信息\(o\)时,我们称这个过程为部分可观测的(partial observable) 的,对应的决策过程即称为部分可观测马尔可夫决策过程 (Partially Observable Markov Decision Processes,POMDP), 部分可观测马尔可夫决策过程是马尔可夫决策过程的一种泛化。部分可观测马尔可夫决策过程依然具有马尔可夫性质,但是假设智能体无法感知环境的状态,只能知道部分观测值。通常用一个七元组描述 \((S, \Omega, O, A, P, R, \gamma)\),其中O为观测空间,\(\Omega(o|s,a)\)为观测概率函数,其他与 MDP 的定义类似。
动作空间/Action Spaces¶
不同的环境对应的动作空间一般是不同的。一般将环境中所有有效动作\(a\) 的集合称之为动作空间 (Action Space)。其中,动作空间又分为离散 (discrete) 动作空间与连续 (continuous) 动作空间。
例如在 Atari 游戏与 SMAC 星际游戏中为离散的动作空间,只可以从有限数量的动作中进行选择,而 MuJoCo 等一些机器人连续控制任务中为连续动作空间,动作空间一般为实值向量区间。
奖励与回报/Reward and Return¶
奖励 (reward) 是智能体所处的环境给强化学习方法的一个学习信号 (signal),当环境发生变化时,奖励函数也会发生变化。奖励函数由当前的状态与智能体的动作决定,表示为\(r_t = R(s_t, a_t)\)。
回报 (Return), 又称为累积折扣奖励,定义为在一个马尔可夫决策过程中从\(t\)时刻开始往后所有奖励的加权和:\(G_t = \sum_{k=0}^{\infty} \gamma^{k} r_{t+k}\)。其中\(\gamma\) 表示折扣因子(衰减因子)体现的是未来的奖励在当前时刻的相对重要性,如果接近0,则表明趋向于只评估当前时刻的奖励,接近于1时表明同时考虑长期的奖励。一般情况下,\(\gamma \in [0,1)\)。在很多现实任务对应环境中的奖励函数可能是稀疏的,即并不是每一个状态下环境都会给予奖励,只有在一段轨迹过后才会给出一个奖励。因此在强化学习中,对奖励函数的设计与学习也是一个重要的方向,对强化学习方法的效果有很大的影响。
策略/Policy¶
策略 (policy) 决定了智能体面对不同的环境状态时采取的动作,是智能体的动作模型。它本质上是一个函数,用于把输入的状态变成动作。策略可分为两种:随机性策略和确定性策略。当策略为确定的 (deterministic),一般用 \(a_t = \mu(s_t)\) 来表示,当策略为随机的 (stochastic),一般表示为 \(\pi(a_t|s_t)\) 。一般情况下,强化学习使用随机性策略,通过引入一定的随机性可以更好地探索环境。
在强化学习中,基于策略梯度的方法显式地需要学习一个参数化表示的策略 (Parameterized policy),用神经网络拟合策略函数,经常使用\(\theta\) 表示神经网络的参数。但基于价值函数的方法则不一定需要显式地学习策略函数,而是通过学习得到的最优动作值函数中推导出策略,即\(a^{*}=\pi^*(a|s)={\arg \max }_a Q^*(s,a)\)。
价值函数/Value Functions¶
状态价值函数 (state value function) 是指智能体在状态 \(s_t\)以及以后的所有时刻都采用策略\(\pi\) 得到的累计折扣奖励(回报)的期望值:
\(V_{\pi}(s) = E_{\pi}[G_t|s_t=s]\)
动作价值函数 (action value function) 是指智能体在状态 \(s_t\)采取动作\(a_t\), 以后的所有时刻都采用策略\(\pi\) 得到的累计折扣奖励(回报)的期望值:
\(Q_{\pi}(s, a) = E_{\pi}[G_t|s_t=s, a_t=a]\)
状态价值函数和行为价值函数的关系:\(V_{\pi}(s) = \sum_{a \in A} \pi(a|s)Q_{\pi}(s,a)\)
我们定义最优策略\(\pi^*\)对应的最优状态值函数与最优动作价值函数分别为\(V^*(s), Q^*(s, a)\)。
最优的状态价值函数与最优的行为价值函数的关系:\(V^*(s)=max_a Q^*(s, a)\)
贝尔曼方程 (Bellman Equations)是强化学习方法的基础,描述的是当前时刻状态的值(动作值)与下一时刻状态的值(动作值)之间的递推关系。
\(V_{\pi}(s) = E_{\pi,P}[r_{t}+\gamma * V_{\pi}(s_{t+1})|S_t=s]\)
\(Q_{\pi}(s, a) = E_{\pi,P}[r_{t}+\gamma * Q_\pi(s_{t+1},a_{t+1})|S_t=s, A_t=a]\)
进一步如果将期望展开,可以写成下面的形式:
其中\(R_{s}^{a}=\mathbb{E}\left[R_{t} \mid S_{t}=s, A_{t}=a\right]\), \(P_{s s^{\prime}}^{a}=\mathbb{P}\left[S_{t+1}=s^{\prime} \mid S_{t}=s, A_{t}=a\right]\)
贝尔曼最优方程 (Bellman Optimality Equations),描述的是当前时刻状态的最优值(最优动作值)与下一时刻状态的最优值(最优动作值)之间的递推关系。
\(V^*(s)=max_a( E[r_{t} + \gamma * V^*(s_{t+1})|s_t=s])\)
\(Q^*(s, a) = E[r_{t}+\gamma * max_{a'}Q^*(s_{t+1},a')|s_t=s, a_t=a]\)
进一步如果将期望展开,可以写成下面的形式:
\(v_{*}(s)=\max _{a} R_{s}^{a}+\gamma \sum_{s^{\prime} \in \mathcal{S}} P_{s s^{\prime}}^{a} v_{*}\left(s^{\prime}\right)\)
\(q^{*}(s, a)=R_{s}^{a}+\gamma \sum_{s^{\prime} \in S} P_{s s^{\prime}}^{a} \max _{a^{\prime}} q^{*}\left(s^{\prime}, a^{\prime}\right)\)
同样的,其中\(R_{s}^{a}=\mathbb{E}\left[R_{t} \mid S_{t}=s, A_{t}=a\right]\), \(P_{s s^{\prime}}^{a}=\mathbb{P}\left[S_{t+1}=s^{\prime} \mid S_{t}=s, A_{t}=a\right]\)。
对于模型已知 (即知道状态转移概率函数和奖励函数) 的系统,值函数可以利用动态规划的方法得到;对于模型未知的系统,可以利用蒙特卡洛的方法或者时间差分的方法得到。
下面分别简介这3类方法:
动态规划 (Dynamic Programming, DP) 方法:
我们知道动态规划适合解决满足最优子结构(optimal substructure)和重叠子问题(overlapping subproblem)两个性质的问题。而给定MDP和策略\(\pi\)求解策略 \(\pi\) 对应的价值函数\(V_\pi\)的问题恰好满足这2个性质,我们可以利用贝尔曼方程,把求解\(V_\pi\)的问题分解成求解不同状态\(s\)的值\(V_\pi(s)\)的子问题。可以把它分解成递归的结构,如果某个问题的子状态能得到一个值,那么它的未来状态因为与子状态是直接相关的,我们也可以将之推算出来。价值函数\(V_\pi(s)\)可以存储并重用子问题的最佳的解。具体地,我们可以直接把贝尔曼期望方程,变成迭代的过程,反复迭代直到收敛。当我们得到上一迭代的 \(V_t\)的时候,就可以通过递推的关系推出下一迭代的值。\(V^{t+1}(s)=\sum_{a \in A} \pi(a \mid s)\left(R(s, a)+\gamma \sum_{s^{\prime} \in S} p\left(s^{\prime} \mid s, a\right) V^{t}\left(s^{\prime}\right)\right)\)。反复迭代,最后得到的 \(V\) 的值就是从 \(V_1\), \(V_2\) , \(V_3\), …, 到最后收敛之后的值\(V_\pi\)。\(V_\pi\)就是当前给定的策略 \(\pi\) 对应的价值函数。
但是 DP 方法必须要求给定环境模型(状态转移函数,奖励函数),而这往往是不现实的,而且 DP 方法很难用于连续状态和动作的环境中。
蒙特卡洛 (Monte Carlo, MC)方法是指我们可以采样大量的轨迹,计算所有轨迹的真实回报\(G_{t}=r_{t}+\gamma r_{t+1}+\gamma^{2} r_{t+2}+\ldots\),然后计算平均值作为Q值的估计。即使用经验平均回报(empirical mean return)的方法来估计期望值。
它不需要马尔可夫决策过程的状态转移函数和奖励函数,也不需要像动态规划那样用自举的方法,只能用在有终止状态的马尔可夫决策过程中。
时序差分 (Temporal Difference, TD)方法时序差分是介于蒙特卡洛和动态规划之间的方法,它是免模型的,不需要马尔可夫决策过程的状态转移函数和奖励函数。可以从不完整的回合中学习,并且结合了自举的思想。最简单的算法是一步时序差分(one-step TD) 即 TD(0)。每往前走一步,就做一步自举,用得到的估计回报(estimated return)\(r_t + \gamma V (s_{t+1})\) 来更新上一时刻的值 \(V (s_t)\): \(V (s_{t})\leftarrow V (s_{t}) + \alpha (r_{t} + \gamma V (s_{t+1})- V (s_{t}))\)
这几种学习值函数的方法的比较如下图所示。
对于表格型的强化学习方法,我们通过迭代更新值函数的表格即可完成对值函数的估计。而很多情况下,如状态空间或动作空间不为离散空间时,值函数无法用一张表格来表示。此时,我们需要利用函数逼近的方法对值函数进行表示。
关于基于值函数(又称为 value-based)的强化学习算法的细节,请参考 DQN, Rainbow 等具体算法文档。
策略梯度/Policy Gradients¶
在基于值函数的方法中,我们希望迭代计算得到最优值函数,然后根据最优值函数得到最优动作;RL 方法中还有另外一大类基于策略梯度的方法,直接学习参数化的最优策略。
下面首先阐述策略梯度定理:
令 \(\tau\) 表示一条轨迹,初始状态分布为 \(\mu\),如果动作是按照策略\(\pi\)选择的,那么轨迹 \(\tau\)的概率分布为:\({Pr}_{\mu}^{\pi}(\tau)=\mu\left(s_{0}\right) \pi\left(a_{0} \mid s_{0}\right) P\left(s_{1} \mid s_{0}, a_{0}\right) \pi\left(a_{1} \mid s_{1}\right) \cdots\)
这条轨迹的累计折扣奖励为:\(R(\tau):=\sum_{t=0}^{\infty} \gamma^{t} r\left(s_{t}, a_{t}\right)\)
策略\(\pi_\theta\)期望最大化的目标为:\(V^{\pi_{\theta}}(\mu)=\mathbb{E}_{\tau \sim {Pr}_{\mu}^{\pi_{\theta}}[R(\tau)]}\)
3种形式的策略梯度公式为:
REINFORCE 形式:
Q值形式:
优势函数形式:
利用策略梯度定理,我们便可以利用采样的样本近似计算策略梯度,直接更新策略网络对应的参数,使策略逐步得到改进。
与基于值函数的RL方法相比,基于策略梯度的方法更加容易收敛到局部最小值,评估单个策略时并不充分,方差较大。
关于基于策略梯度(又称为 policy-based)的强化学习算法的细节,请参考PPO等具体算法文档。
演员-评论家/Actor Critic¶
Critic,参数化动作值函数,进行策略的价值评估。
Actor,参数化的策略函数,按照 Critic 部分得到的价值,利用策略梯度指导策略函数参数的更新。
总结来说,Actor Critic是一种既学习价值函数也学习策略函数的方法,结合了以上两种方法的优点。
基于这个框架下的各种算法,既可以去适应不同的动作空间与状态空间的问题,也可以对不同的策略空间中找到最优策略。
关于基于 Actor Critic 的强化学习算法的细节,请参考 A2C, DDPG, TD3, SAC 等具体算法文档。
基于模型/Model-based RL¶
在 model-free 的 RL 方法中,value-based方法先学习值函数(利用 MC 或 TD 方法),再从最优值函数中提取最优策略,policy-based 方法直接优化策略。
而 model-based 方法的重点在于如何学习环境模型 (environment model) 和如何利用学习好的模型来学习值函数或策略。通过学习环境模型,可以帮助我们提高强化学习方法的样本效率 (sample efficiency)。
环境模型可以定义为状态转移分布和奖励函数组成的元组: \(M=(P,R), 其中P(s_{t+1}|s_t, a_t)表示状态转移函数, R(r_{t}|s_t, a_t)\)表示奖励函数。
根据模型学习方法和使用方法的不同,可以有各种各样的 model-based RL 算法。
在学习好环境模型后,主要有两种使用方法,一种是通过学到的模型生成一些仿真轨迹,在这些仿真轨迹上学习最优值函数进而得到最优策略;另一种是在学到的模型上直接优化策略。
Q&A¶
强化学习 (Reinforcement Learning) 与监督学习 (Supervised Learning) 的本质区别在于?
监督学习是从大量有标签的数据集中进行模式和特征的学习,样本通常是需要满足独立同分布的假设。
强化学习不需要带标签的数据集,而是建立在智能体与环境交互的基础上,强化学习会试错探索,它通过探索环境来获取对环境的理解。
用于强化学习训练的样本是有时间关系的序列样本,而且样本的产生与智能体的策略相关。
强化学习中没有强的监督信号,只有稀疏的,延迟的奖励信号。
什么是 exploration and exploitation?我们通常使用哪些方法平衡 exploration and exploitation?
Exploration 指的是RL中的智能体需要不断的去探索环境的不同状态动作空间, 尽可能收集到多样化的样本用于强化学习训练,而 exploitation 指的是智能体需要利用好已经获得的“知识”,去选择当前状态下收益高的动作。如果 exploitation 太多,那么模型比较容易陷入局部最优,但是 exploration 太多,模型收敛速度太慢。如何在 exploitation-exploration 中取得平衡,以获得一种累计折扣奖励最高的最优策略,是强化学习中的一个核心问题。
什么是 model based RL 和 model free RL,两者区别是什么?
Model based RL 算法指智能体会学习环境的模型 (通常包括状态转移函数和奖励函数),并利用环境模型来进行策略迭代或值迭代,而 model free RL 算法则不需要对环境进行建模。蒙特卡洛和 TD 算法隶属于 model-free RL,因为这两类算法不需要算法建模具体环境。而动态规划属于 model-based RL,因为使用动态规划需要完备的环境模型。
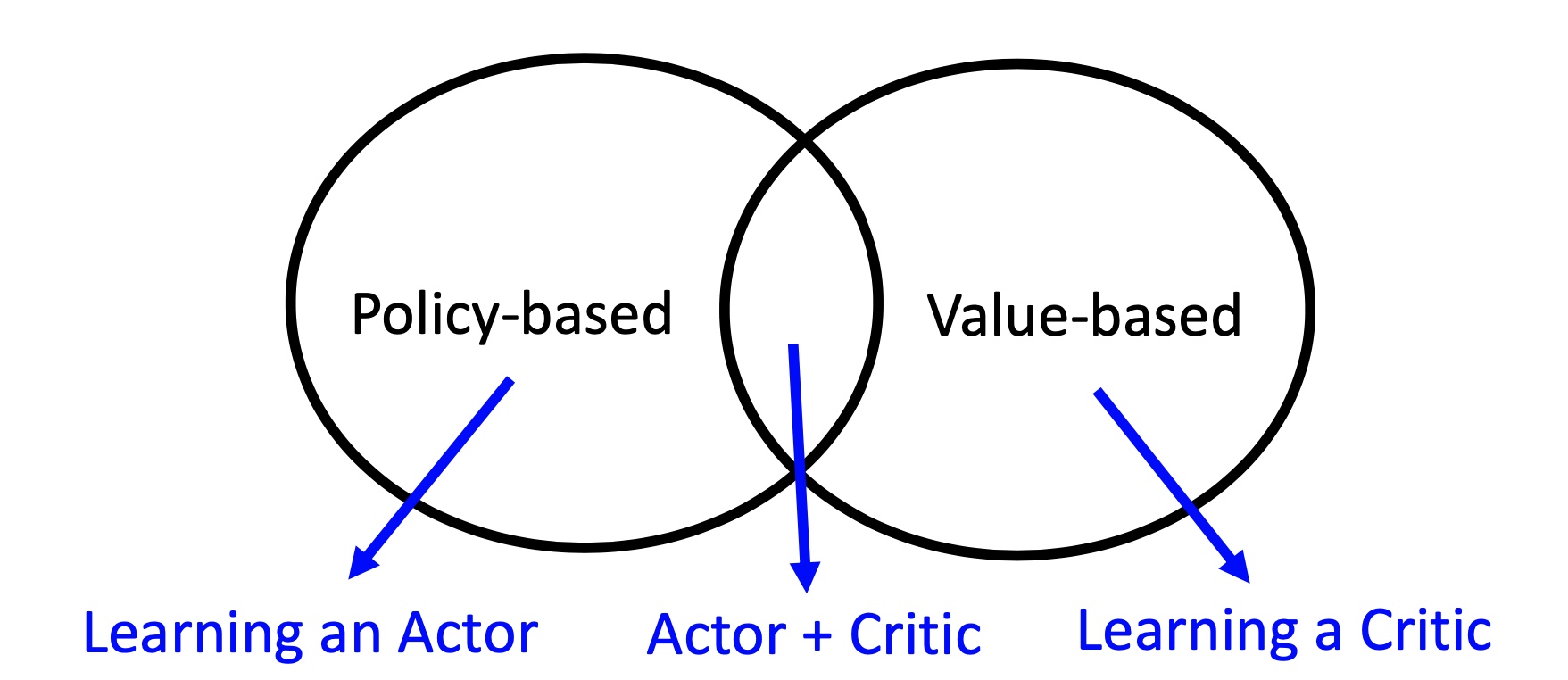
value-based, policy-based,actor-critic,三者分别是什么含义?
value-based 就是学习值函数(或动作值函数),评价一个状态(状态动作对)的价值,policy-based 是指直接学习一个参数化的策略网络,一般通过策略梯度定理进行优化,而 actor-critic 是同时学习值网络和策略网络,是前面两者的结合,集成了值迭代和策略迭代范式,是解决实际问题时最常考虑的框架。 具体关系如下图所示:
什么是 on-policy 和 off-policy,两者区别是什么?
On-policy 是使用当前的策略生成的样本进行训练,产生数据样本的策略和用于当前待评估和改进的策略是相同的。
Off-policy 则是指在更新当前策略时可以用到之前旧的策略产生的样本,产生数据样本的策略和当前待评估和改进策略是不同的。
一般来讲,on-policy 很难平衡探索与利用的问题,容易学习到局部最优解,虽然对整体策略的更新更稳定但是降低了学习的效率。off-policy 的优势在于重复利用数据进行训练,但是收敛速度与稳定性不如 on-policy 的算法。值得注意的是, Soft Actor Critic 提出的最大熵强化学习算法极大的提高了 off-policy 算法的稳定性和性能。
什么是 online training 和 offline training?我们通常如何实现 offline training?
Online training 指的是用于 RL 训练的数据是智能体与环境交互实时产生的。 Offline training 即是训练时智能体不与环境进行交互,而是直接在给定的固定数据集上进行训练, 比如 behavior cloning 就是经典的 Offline training 算 法。 我们通常在固定数据集上采样一个 batch 用于 RL 训练,因此 offline RL 又称为 Batch RL。具体参考我们的 offline RL 文档
为什么要使用 replay buffer? experience replay 作用在哪里?
智能体与环境交互后产生的数据往往是具有很强的时序相关信息的,由于随机梯度下降通常要求训练的数据符合 i.i.d. 假设,因此将智能体与环境交互后产生的数据直接用于 RL 训练往往存在稳定性问题。
有了 replay buffer 后,我们可以将智能体收集的样本存入 buffer 中,在之后训练时通过某种方式从 buffer 中采样出 mini-batch 的 experience 用于 RL 训练。
当 replay buffer 中的数据足够多时,随机抽样得到的数据就能接近 i.i.d.,使得 RL 训练更加稳定。同时由于 experience replay 的存在,智能体收集的样本不是用过就丢弃,结合 off-policy 的算法,能够多次重复利用过去的经验,提高了样本效率 (data efficiency)。
强化学习目前的应用场景有哪些?
强化学习已经在游戏领域(Atari 游戏,星际争霸,王者荣耀,象棋,围棋等)取得了比肩人类甚至超越人类的成就。在现实应用中,强化学习在互联网推荐,搜索方面有丰富的应用场景。除此之外,强化学习也被应用于自动驾驶,机器人控制等控制系统中。在医疗,生物,量化交易等领域,强化学习可以用于处理更多复杂的决策问题。