C51¶

概述¶

C51 最初是在 A Distributional Perspective on Reinforcement Learning 中提出的，与以往的研究不同，C51 评估了 q 值的完整分布，而不仅仅是期望值。作者设计了一个分布式 Bellman 算子，它保留了值分布中的多峰性，被认为能够实现更稳定的学习，并减轻从非稳态策略学习的负面影响。

核心要点¶

C51 是一种 无模型（model-free） 和 基于值（value-based） 的强化学习算法。
C51 仅 支持离散动作空间 。
C51 是一种 异策略（off-policy） 算法。
通常, C51 使用 eps-greedy 或 多项式采样 进行探索。
C51 可以与循环神经网络 (RNN) 结合使用。

伪代码¶

Note

C51 使用离散分布来建模值分布，其支持集合为N个原子: \(z_i = V_\min + i * delta, i = 0,1,...,N-1\) 和　\(delta = (V_\max - V_\min) / N\) 。每个原子　\(z_i\) 都有一个参数化的概率 \(p_i\) 。C51 的贝尔曼更新将 \(r + \gamma * z_j^{\left(t+1\right)}\) 的分布投影到分布 \(z_i^t\) 上。

关键方程或关键框图¶

C51 的贝尔曼方程的目标是通过将返回分布 \(r + \gamma * z_j\) 投影到当前分布 \(z_i\) 上来得到的. 给定一个采样出来的状态转移 \((x, a, r, x')\)，我们为每个原子　\(z_j\) 计算贝尔曼更新 \(Tˆz_j := r + \gamma z_j\) ，然后将其概率 \(p_{j}(x', \pi(x'))\) 分配给其相邻的原子 \(p_{i}(x, \pi(x))\):

\[\left(\Phi \hat{T} Z_{\theta}(x, a)\right)_{i}=\sum_{j=0}^{N-1}\left[1-\frac{\left|\left[\hat{\mathcal{T}} z_{j}\right]_{V_{\mathrm{MIN}}}^{V_{\mathrm{MAX}}}-z_{i}\right|}{\Delta z}\right]_{0}^{1} p_{j}\left(x^{\prime}, \pi\left(x^{\prime}\right)\right)\]

扩展¶

C51 可以和以下模块结合:
- 优先经验回放 (Prioritized Experience Replay)
- 多步时序差分 (TD) 损失
- 双目标网络 (Double Target Network)
- Dueling head
- 循环神经网络 (RNN)

实现¶

Tip

我们的 C51 基准结果使用了与 DQN 相同的超参数，(除 n_atom 这个 C51 特有的参数以外)，这也是配置 C51 的通用方法。

C51 的默认配置如下:

class ding.policy.c51.C51Policy(cfg: EasyDict, model: Module | None = None, enable_field: List[str] | None = None)[source]

Overview:

Policy class of C51 algorithm.

Config:

ID	Symbol	Type	Default Value	Description	Other(Shape)
1	`type`	str	c51	RL policy register name, refer to registry `POLICY_REGISTRY`	this arg is optional, a placeholder
2	`cuda`	bool	False	Whether to use cuda for network	this arg can be diff- erent from modes
3	`on_policy`	bool	False	Whether the RL algorithm is on-policy or off-policy
4	`priority`	bool	False	Whether use priority(PER)	priority sample, update priority
5	`model.v_min`	float	-10	Value of the smallest atom in the support set.
6	`model.v_max`	float	10	Value of the largest atom in the support set.
7	`model.n_atom`	int	51	Number of atoms in the support set of the value distribution.
8	`other.eps` `.start`	float	0.95	Start value for epsilon decay.
9	`other.eps` `.end`	float	0.1	End value for epsilon decay.
10	`discount_` `factor`	float	0.97, [0.95, 0.999]	Reward’s future discount factor, aka. gamma	may be 1 when sparse reward env
11	`nstep`	int	1,	N-step reward discount sum for target q_value estimation
12	`learn.update` `per_collect`	int	3	How many updates(iterations) to train after collector’s one collection. Only valid in serial training	this args can be vary from envs. Bigger val means more off-policy

C51 使用的网络接口定义如下:

class ding.model.template.q_learning.C51DQN(obs_shape: int | SequenceType, action_shape: int | SequenceType, encoder_hidden_size_list: SequenceType = [128, 128, 64], head_hidden_size: int | None = None, head_layer_num: int = 1, activation: Module | None = ReLU(), norm_type: str | None = None, v_min: float | None = -10, v_max: float | None = 10, n_atom: int | None = 51)[source]

Overview:: The neural network structure and computation graph of C51DQN, which combines distributional RL and DQN. You can refer to https://arxiv.org/pdf/1707.06887.pdf for more details. The C51DQN is composed of encoder and head. encoder is used to extract the feature of observation, and head is used to compute the distribution of Q-value.
Interfaces:: __init__, forward

Note

Current C51DQN supports two types of encoder: FCEncoder and ConvEncoder.

forward(x: Tensor) → Dict[source]

Overview:

C51DQN forward computation graph, input observation tensor to predict q_value and its distribution.

Arguments:

x (torch.Tensor): The input observation tensor data.

Returns:

outputs (Dict): The output of DQN’s forward, including q_value, and distribution.

ReturnsKeys:

logit (torch.Tensor): Discrete Q-value output of each possible action dimension.
distribution (torch.Tensor): Q-Value discretized distribution, i.e., probability of each uniformly spaced atom Q-value, such as dividing [-10, 10] into 51 uniform spaces.

Shapes:

x (torch.Tensor): \((B, N)\), where B is batch size and N is head_hidden_size.
logit (torch.Tensor): \((B, M)\), where M is action_shape.
distribution(torch.Tensor): \((B, M, P)\), where P is n_atom.

Examples:

>>> model = C51DQN(128, 64)  # arguments: 'obs_shape' and 'action_shape'
>>> inputs = torch.randn(4, 128)
>>> outputs = model(inputs)
>>> assert isinstance(outputs, dict)
>>> # default head_hidden_size: int = 64,
>>> assert outputs['logit'].shape == torch.Size([4, 64])
>>> # default n_atom: int = 51
>>> assert outputs['distribution'].shape == torch.Size([4, 64, 51])

Note

For consistency and compatibility, we name all the outputs of the network which are related to action selections as logit.

Note

For convenience, we recommend that the number of atoms should be odd, so that the middle atom is exactly the value of the Q-value.

基准测试¶

Benchmark and comparison of c51 algorithm¶
environment	best mean reward	config link	comparison
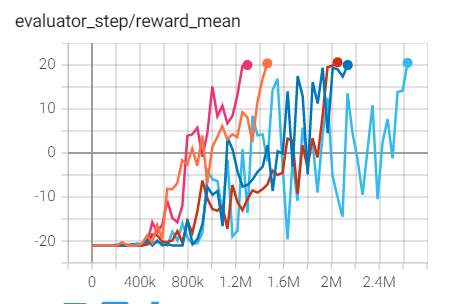
Pong (PongNoFrameskip-v4)	20.6	config_link_p	Tianshou(20)
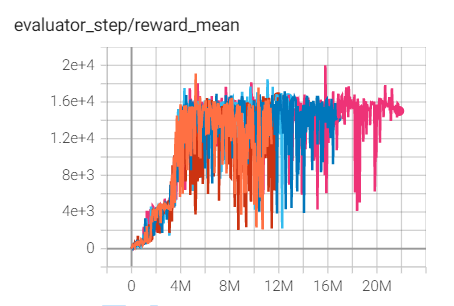
Qbert (QbertNoFrameskip-v4)	20006	config_link_q	Tianshou(16245)
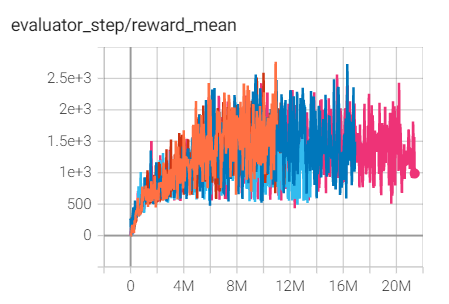
SpaceInvaders (SpaceInvadersNoFrame skip-v4)	2766	config_link_s	Tianshou(988.5)

P.S.：

上述结果是在五个不同的随机种子（0、1、2、3、4）上运行相同配置的实验得出的。
对于像 DQN 这样的离散动作空间算法，通常使用 Atari 环境集进行测试（包括子环境 Pong ），而 Atari 环境通常通过训练10M个环境步骤的最高平均奖励来评估。关于 Atari 的更多细节，请参考 Atari Env Tutorial 。

其他开源实现¶

Tianshou