DQN

综述

传统的 Q-learning 维护一张 M*N 的Q值表（其中 M表示状态个数，N表示动作个数），通过贝尔曼方程（Bellman equation）来迭代更新 Q-value。这种算法在状态/动作空间变得很大的时候就会出现维度灾难的问题。而DQN与传统强化学习方法不同，它将 Q-learning 与深度神经网络相结合，使用深度神经网络来估计 Q 值，并通过计算时序差分（TD, Temporal-Difference） 损失，利用梯度下降算法进行更新，从而在高维空间的问题决策中（例如Atari游戏）达到了媲美甚至超过人类玩家的水平。

快速了解

1. DQN 是一个 无模型（model-free） 且 基于值函数（value-based） 的强化学习算法。

2. DQN 只支持 离散（discrete） 动作空间。

3. DQN 是一个 异策略（off-policy） 算法.

4. 通常，DQN 使用 epsilon贪心（eps-greedy） 或 多项分布采样（multinomial sample） 来做探索（exploration）。

5. DQN + RNN = DRQN

6. DI-engine 中实现的 DQN 支持 多维度离散（multi-discrete） 动作空间，即在一个step下执行多个离散动作。

重要公示/重要图示

DQN 中的 TD-loss 是：

\[\mathrm{L}(w)=\mathbb{E}\left[(\underbrace{r+\gamma \max _{a^{\prime}} Q_{\text {target }}\left(s^{\prime}, a^{\prime}, \theta^{-}\right)}-Q(s, a, \theta))^{2}\right]\]

其中目标网络 \(Q_{\text {target}}\) ，带有参数 \(\theta^{-}\) ，与在线网络相同，只是它的参数会每 target_update_freq 个环境步数从在线网络复制更新一次（超参数 target_update_freq 可以在配置文件中修改。请参考 TargetNetworkWrapper 了解更多详情）。

伪代码

Note

与发表在 Nature 的版本相比，现代的 DQN 在算法和实现方面都得到了显著改进。譬如，在算法部分，TD-loss, PER, n-step, target network and dueling head 等技巧被广泛使用，感兴趣的读者可参考论文 Rainbow: Combining Improvements in Deep Reinforcement Learning。

扩展

DQN 可以和以下方法相结合：

• 优先级经验回放 （PER，Prioritized Experience Replay ）

  Prioritized Experience Replay 用一种特殊定义的“优先级”来代替经验回放池中的均匀采样。该优先级可由各种指标定义，如绝对TD误差、观察的新颖性等。通过优先采样，DQN的收敛速度和性能可以得到很大的提高。

  优先级经验回放（PER）有两种实现方式，其中一种较常用方式的伪代码如下图所示：

  

  在DI-engine中，PER可以通过修改配置文件中的 priority 和 priority_IS_weight 两个字段来控制，具体的代码实现可以参考 PER code 。具体的示例讲解可以参考 PER example

• 多步（Multi-step） TD-loss

  在 Single-step TD-loss 中，Q-learning 通过贝尔曼方程更新 \(Q(s,a)\):

  \[r(s,a)+\gamma \max_{a^{'}}Q(s',a')\]

  在 Multi-step TD-loss 中，贝尔曼方程是:

  \[\sum_{t=0}^{n-1}\gamma^t r(s_t,a_t) + \gamma^n \max_{a^{'}}Q(s_n,a')\]

  Note

  在DQN中使用 Multi-step TD-loss 有一个潜在的问题：采用 epsilon 贪心收集数据时， Q值的估计是有偏的。 因为t >= 1时，\(r(s_t,a_t)\) 是在 epsilon-greedy 策略下采样的，而不是通过正在学习的策略本身来采样。但实践中发现 Multi-step TD-loss 与 epsilon-greedy 结合使用，一般都可以明显提升智能体的最终性能。

  在DI-engine中，Multi-step TD-loss 可以通过修改配置文件中的 nstep 字段来控制，详细的损失函数计算代码可以参考 nstep code 中的 q_nstep_td_error

• 目标网络（target network/Double DQN）

  Double DQN, 在 Deep Reinforcement Learning with Double Q-learning 中被提出，是 DQN 的一种常见变种。

  标准 Q 学习或 DQN 中在计算目标网络时的 max 算子使用同一个的 Q 值来选择和评估动作。这使得它选择的动作的价值更有可能被高估，从而导致过度乐观的价值估计。为了防止这种情况，我们可以将选择与评估分离。更具体地说，以下两个公式展示了二者的差异：

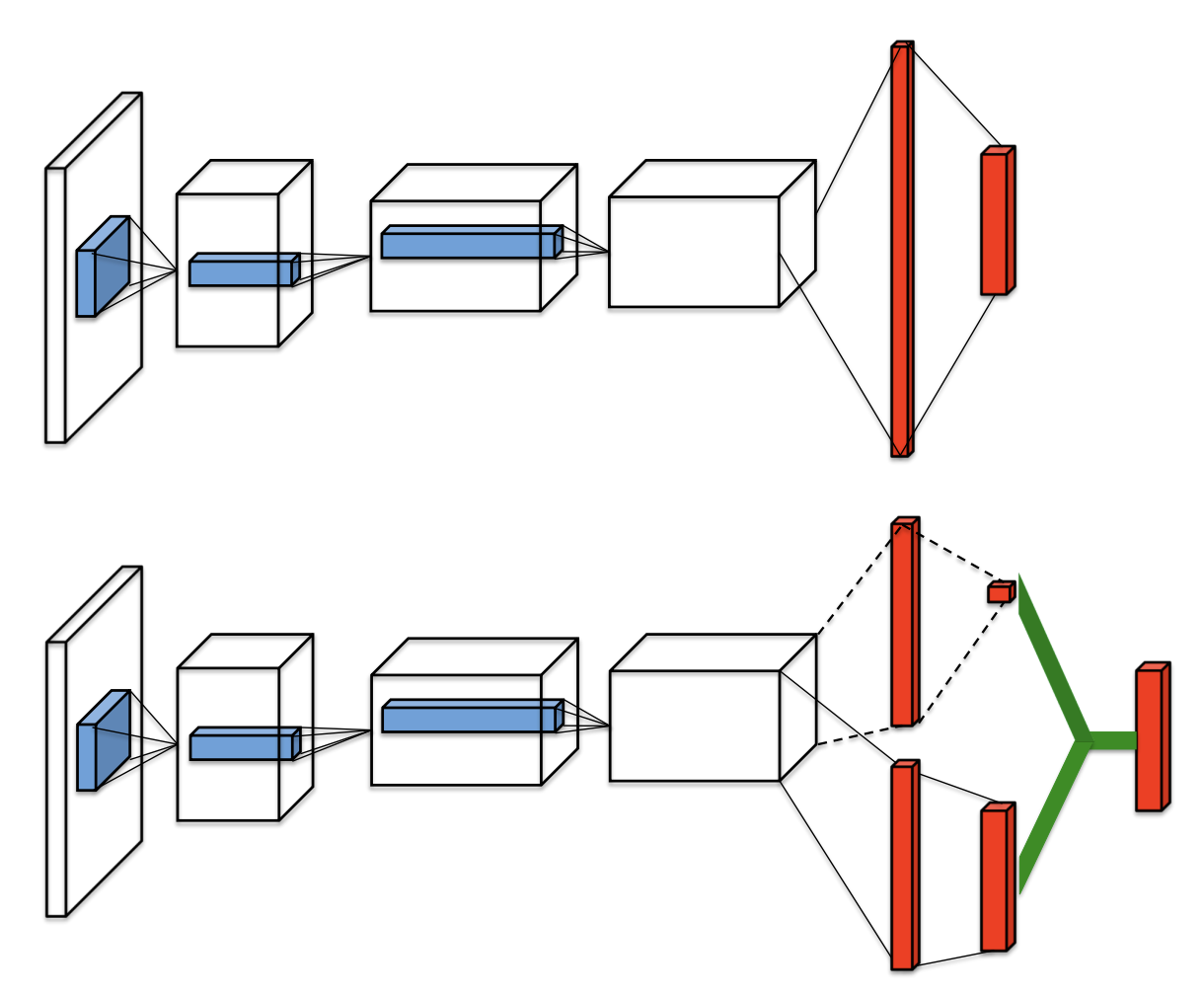
  （1）标记的Q-learning和（2）标记的Double DQN中的目标如下图所示：

  

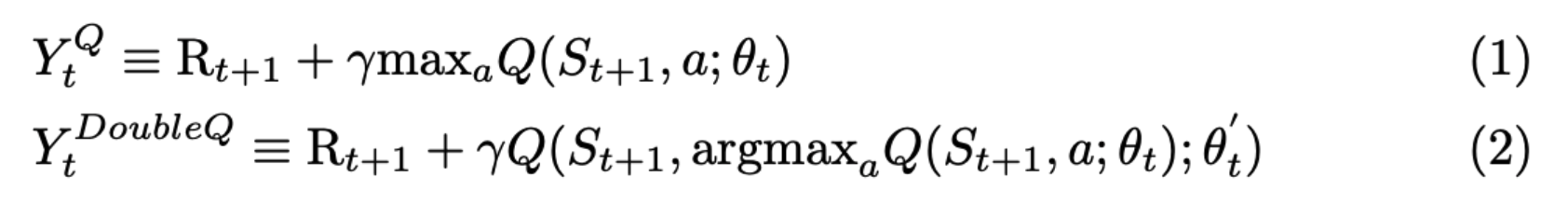
  区别于传统DQN，Double DQN中的目标网络不会选择当前网络中离散动作空间中的最大Q值，而是首先查找 在线网络 中Q值最大的动作（对应上面公式中的 \(argmax_a Q(S_{t+1},a;\theta_t)\)），然后根据该动作从 目标网络 计算得到Q值 (对应上面公示中的 \(Q(S_{t+1},argmax_a Q(S_{t+1},a;\theta_t);\theta'_t)\)）。

  综上所述，Double Q-learning 可以抑制 Q 值的高估，从而减少相关的负面影响。

  DI-engine 默认实现并使用 Double DQN ，没有关闭选项。

  Note

  过高估计可能是由函数近似误差（近似Q值的神经网络）、环境噪声、数值不稳定等原因造成的。

• Dueling head (Dueling Network Architectures for Deep Reinforcement Learning)

  Dueling head 结构通过对每个动作的状态-价值和优势的分解，并由上述两个部分构建最终的Q值，从而更好地评估一些与动作选择无关的状态的价值。下图展示了具体的分解结构（图片来自论文 Dueling Network Architectures for Deep Reinforcement Learning）：

  

  在DI-engine中，Dueling head 可以通过修改配置文件中模型部分的 dueling 字段来控制，具体网络结构的实现可以参考 Dueling Head 中的 DuelingHead

• RNN (DRQN, R2D2)

  DQN与RNN结合的方法，可以参考本系列文档中的 R2D2部分

实现

DQNPolicy 的默认 config 如下所示：

class ding.policy.dqn.DQNPolicy(cfg: EasyDict, model: Module | None = None, enable_field: List[str] | None = None)

Overview:

Policy class of DQN algorithm, extended by Double DQN/Dueling DQN/PER/multi-step TD.

Config:

ID	Symbol	Type	Default Value	Description	Other(Shape)
1	type	str	dqn	RL policy register name, refer to registry POLICY_REGISTRY	This arg is optional, a placeholder
2	cuda	bool	False	Whether to use cuda for network	This arg can be diff- erent from modes
3	on_policy	bool	False	Whether the RL algorithm is on-policy or off-policy
4	priority	bool	False	Whether use priority(PER)	Priority sample, update priority
5	priority_IS _weight	bool	False	Whether use Importance Sampling Weight to correct biased update. If True, priority must be True.
6	discount_ factor	float	0.97, [0.95, 0.999]	Reward’s future discount factor, aka. gamma	May be 1 when sparse reward env
7	nstep	int	1, [3, 5]	N-step reward discount sum for target q_value estimation
8	model.dueling	bool	True	dueling head architecture
9	model.encoder _hidden _size_list	list (int)	[32, 64, 64, 128]	Sequence of hidden_size of subsequent conv layers and the final dense layer.	default kernel_size is [8, 4, 3] default stride is [4, 2 ,1]
10	model.dropout	float	None	Dropout rate for dropout layers.	[0,1] If set to None means no dropout
11	learn.update per_collect	int	3	How many updates(iterations) to train after collector’s one collection. Only valid in serial training	This args can be vary from envs. Bigger val means more off-policy
12	learn.batch_ size	int	64	The number of samples of an iteration
13	learn.learning _rate	float	0.001	Gradient step length of an iteration.
14	learn.target_ update_freq	int	100	Frequence of target network update.	Hard(assign) update
15	learn.target_ theta	float	0.005	Frequence of target network update. Only one of [target_update_freq, target_theta] should be set	Soft(assign) update
16	learn.ignore_ done	bool	False	Whether ignore done for target value calculation.	Enable it for some fake termination env
17	collect.n_sample	int	[8, 128]	The number of training samples of a call of collector.	It varies from different envs
18	collect.n_episode	int	8	The number of training episodes of a call of collector	only one of [n_sample ,n_episode] should be set
19	collect.unroll _len	int	1	unroll length of an iteration	In RNN, unroll_len>1
20	other.eps.type	str	exp	exploration rate decay type	Support [‘exp’, ‘linear’].
21	other.eps. start	float	0.95	start value of exploration rate	[0,1]
22	other.eps. end	float	0.1	end value of exploration rate	[0,1]
23	other.eps. decay	int	10000	decay length of exploration	greater than 0. set decay=10000 means the exploration rate decay from start value to end value during decay length.

其中使用的神经网络接口如下所示：

class ding.model.template.q_learning.DQN(obs_shape: int | SequenceType, action_shape: int | SequenceType, encoder_hidden_size_list: SequenceType = [128, 128, 64], dueling: bool = True, head_hidden_size: int | None = None, head_layer_num: int = 1, activation: Module | None = ReLU(), norm_type: str | None = None, dropout: float | None = None, init_bias: float | None = None)

Overview:

The neural nework structure and computation graph of Deep Q Network (DQN) algorithm, which is the most classic value-based RL algorithm for discrete action. The DQN is composed of two parts: encoder and head. The encoder is used to extract the feature from various observation, and the head is used to compute the Q value of each action dimension.

Interfaces:

__init__, forward.

Note

Current DQN supports two types of encoder: FCEncoder and ConvEncoder, two types of head: DiscreteHead and DuelingHead. You can customize your own encoder or head by inheriting this class.

forward(x: Tensor) → Dict

Overview:

DQN forward computation graph, input observation tensor to predict q_value.

Arguments:

• x (torch.Tensor): The input observation tensor data.

Returns:

• outputs (Dict): The output of DQN’s forward, including q_value.

ReturnsKeys:

• logit (torch.Tensor): Discrete Q-value output of each possible action dimension.

Shapes:

• x (torch.Tensor): \((B, N)\), where B is batch size and N is obs_shape

• logit (torch.Tensor): \((B, M)\), where B is batch size and M is action_shape

Examples:

>>> model = DQN(32, 6)  # arguments: 'obs_shape' and 'action_shape'
>>> inputs = torch.randn(4, 32)
>>> outputs = model(inputs)
>>> assert isinstance(outputs, dict) and outputs['logit'].shape == torch.Size([4, 6])

Note

For consistency and compatibility, we name all the outputs of the network which are related to action selections as logit.

实验 Benchmark

Benchmark and comparison of dqn algorithm

environment	best mean reward	evaluation results	config link	comparison
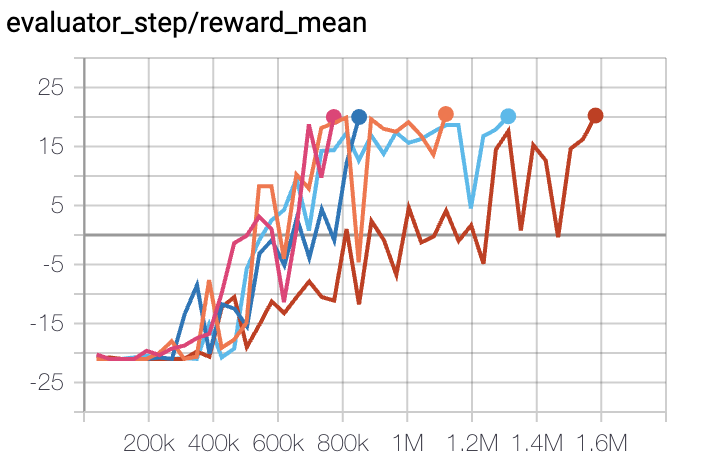
Pong (PongNoFrameskip-v4)	20		config_link_p	Tianshou(20) Sb3(20)
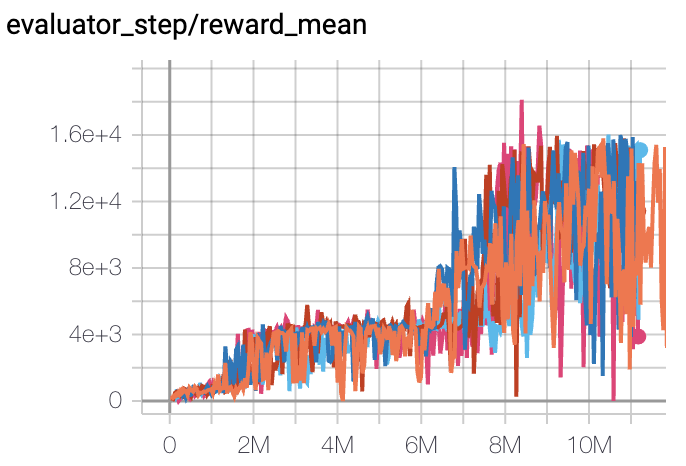
Qbert (QbertNoFrameskip-v4)	17966		config_link_q	Tianshou(7307) Rllib(7968) Sb3(9496)
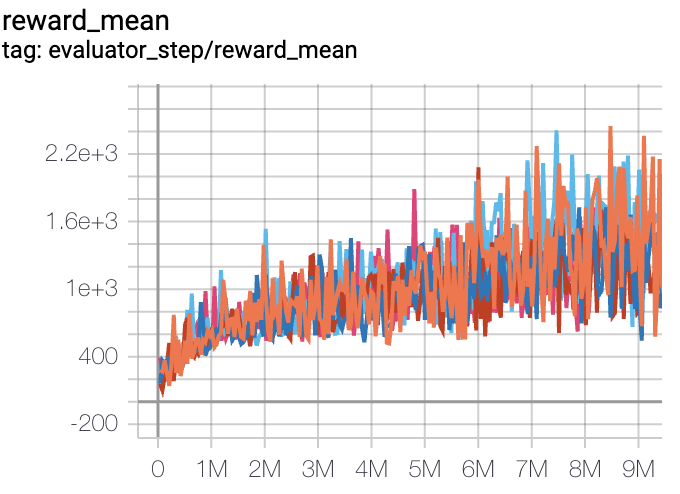
SpaceInvaders (SpaceInvadersNoFrameskip-v4)	2403		config_link_s	Tianshou(812) Rllib(1001) Sb3(622)

注：

1. 以上结果是在5个不同的随机种子（即0，1，2，3，4）运行相同的配置得到

2. 对于DQN这样的离散动作空间算法，一般选择Atari环境集进行测试（其中包括子环境Pong等），而Atari环境，一般是通过训练10M个env_step下所得的最高平均奖励来进行评价，详细的环境信息可以查看 Atari环境的介绍文档

参考文献

• Mnih, Volodymyr, et al. “Human-level control through deep reinforcement learning.” nature 518.7540 (2015): 529-533.

• Wang, Z., Schaul, T., Hessel, M., Hasselt, H., Lanctot, M., & Freitas, N. (2016, June). Dueling network architectures for deep reinforcement learning. In International conference on machine learning (pp. 1995-2003). PMLR.

• Van Hasselt, H., Guez, A., & Silver, D. (2016, March). Deep reinforcement learning with double q-learning. In Proceedings of the AAAI conference on artificial intelligence (Vol. 30, No. 1).

• Schaul, T., Quan, J., Antonoglou, I., & Silver, D. (2015). Prioritized experience replay. arXiv preprint arXiv:1511.05952.