EDAC

Overview

Offline reinforcement learning (RL) is a re-emerging area of study that aims to learn behaviors using large, previously collected datasets, without further environment interaction. It has the potential to make tremendous progress in a number of real-world decision-making problems where active data collection is expensive (e.g., in robotics, drug discovery, dialogue generation, recommendation systems) or unsafe/dangerous (e.g., healthcare, autonomous driving, or education). Besides, the quantities of data that can be gathered online are substantially lower than the offline datasets. Such a paradigm promises to resolve a key challenge to bringing reinforcement learning algorithms out of constrained lab settings to the real world.

However, directly utilizing existing value-based off-policy RL algorithms in an offline setting generally results in poor performance, due to issues with bootstrapping from out-of-distribution actions and overfitting. Thus, many constrain techniques (e.g. policy constraint; conservative estimation; uncertainty estimation) are added to basic online RL algorithms. Uncertainty-Based Offline Reinforcement Learning with Diversified Q-Ensemble (EDAC), first proposed in Uncertainty-Based Offline Reinforcement Learning with Diversified Q-Ensemble, is one of them which penalty out-of-distribution(OOD) action by adding more critic networks.

Quick Facts

1. EDAC is an offline uncertainty estimation RL algorithm.

2. EDAC can be implemented with less than 20 lines of code on top of a number of SAC RL algorithms

3. EDAC supports continuous action spaces.

Key Equations or Key Graphs

EDAC show that clipped Q-learning \(min_{j=1,2}Q(s,a)\) can penalty OOD action by add the number of critic. Therefore EDAC can be implemented by ensembleing Q-network on standard SAC RL algorithm and add a penalty term to penalty OOD action.

In general, for the EDAC, the penalty term is following:

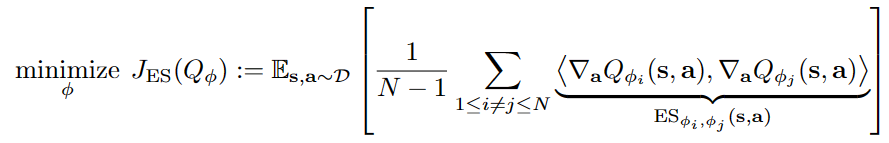
By adding above penalty term, the algorithm can minimize the number of necessary critics to achieve higher computational efficiency while maintaining good performance. This term compute the inner-product of gradients of Q-values of in-dataset state-actions.

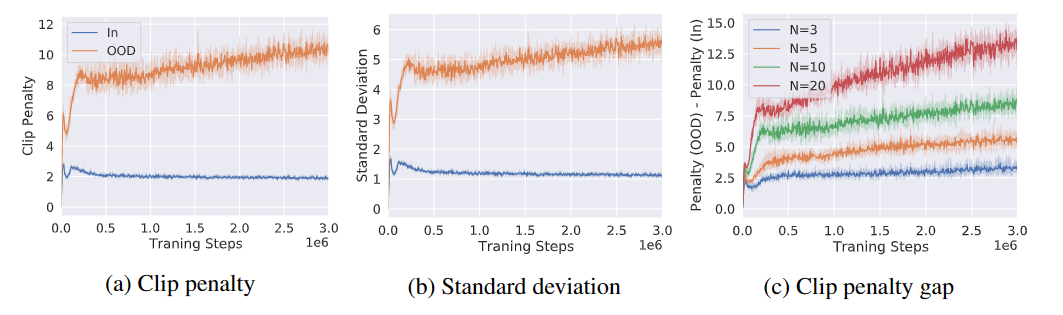
EDAC show the importance of clipped Q-learning by increasing the number of Q-networks in SAC algorithm. By computing the clipe penalty and standard deviation of OOD action adn in-dataset action, paper show why algorithm will perform better by increasing the number of Q-network. The figure of these results is as following:

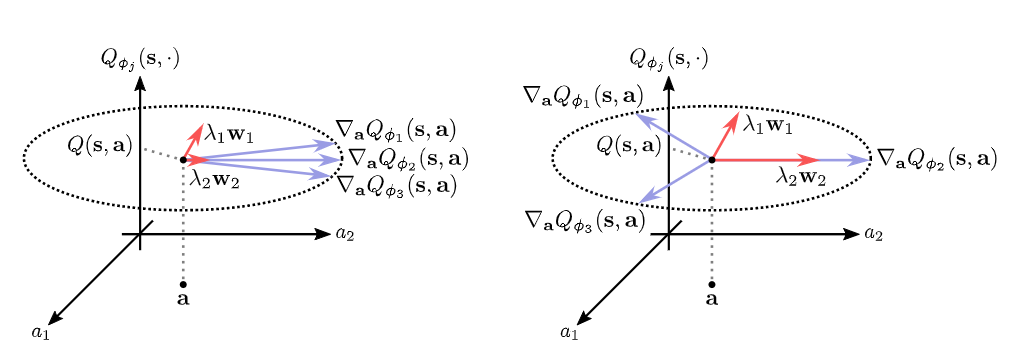
In the figure below, paper shows the gradients of Q-value of OOD action, where the red vector indicates the direction under OOD actions. We find that if the variance of Q-value of OOD actions is small, then it will receive a smaller penalty during gradient descent. This further explains why increasing the number of critics can penalize OOD actions, and also indicates the direction for later improvement in the paper.

Althought increasing the number of Q-networks can improve performance, too many Q networks will become a burden. Therefore, EDAC add a penalty term to reduce the number of critics. Using first-order Taylor approximate, he sample variance of the Q-values at an OOD action along wcan be represented as following:

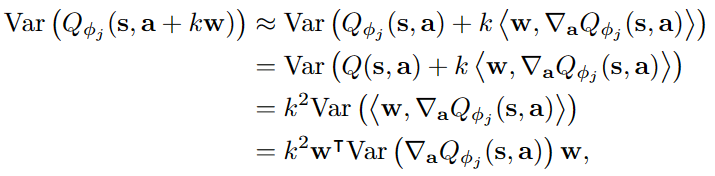
To increasing the variance of Q-values effectively for near-distribution OOD actions, EDAC maximize the following equation:

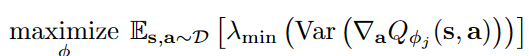
There are several methods to compute the smallest eigenvalue, such as the power method or the QR algorithm. However, these iterative methods require constructing huge computation graphs, which makes optimizing the eigenvalue using back-propagation inefficient. Instead, we aim to maximize the sum of all eigenvalues, which is equal to the total variance. Above equation is equivalent to minimizing the equation of first figure.

Pseudo-code

The pseudo-code is shown in Algorithm 1, with differences from conventional actor critic algorithms (e.g., SAC) in blue

Implementations

The default config of EDACPolicy is defined as follows:

class ding.policy.edac.EDACPolicy(cfg: EasyDict, model: Module | None = None, enable_field: List[str] | None = None)

Overview:

Policy class of EDAC algorithm. Paper link: https://arxiv.org/pdf/2110.01548.pdf

Config:

ID	Symbol	Type	Default Value	Description	Other(Shape)
1	type	str	td3	RL policy register name, refer to registry POLICY_REGISTRY	this arg is optional, a placeholder
2	cuda	bool	True	Whether to use cuda for network
3	random_ collect_size	int	10000	Number of randomly collected training samples in replay buffer when training starts.	Default to 10000 for SAC, 25000 for DDPG/ TD3.
4	model.policy_ embedding_size	int	256	Linear layer size for policy network.
5	model.soft_q_ embedding_size	int	256	Linear layer size for soft q network.
6	model.emsemble _num	int	10	Number of Q-ensemble network	is False.
7	learn.learning _rate_q	float	3e-4	Learning rate for soft q network.	Defalut to 1e-3, when model.value_network is True.
8	learn.learning _rate_policy	float	3e-4	Learning rate for policy network.	Defalut to 1e-3, when model.value_network is True.
9	learn.learning _rate_value	float	3e-4	Learning rate for policy network.	Defalut to None when model.value_network is False.
10	learn.alpha	float	1.0	Entropy regularization coefficient.	alpha is initiali- zation for auto alpha, when auto_alpha is True
11	learn.eta	bool	True	Parameter of EDAC algorithm	Defalut to 1.0
12	learn. auto_alpha	bool	True	Determine whether to use auto temperature parameter alpha.	Temperature parameter determines the relative importance of the entropy term against the reward.
13	learn.- ignore_done	bool	False	Determine whether to ignore done flag.	Use ignore_done only in halfcheetah env.
14	learn.- target_theta	float	0.005	Used for soft update of the target network.	aka. Interpolation factor in polyak aver aging for target networks.

Benchmark

environment	best mean reward	evaluation results	config link	comparison
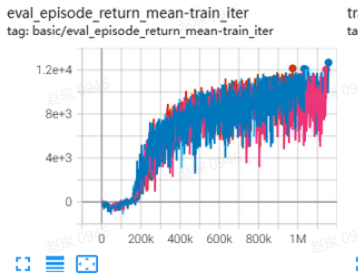
HalfCheetah (Medium Expert)	92.5 \(\pm\) 9.9		config_link_ha	EDAC Repo (106.3 \(\pm\) 1.9)
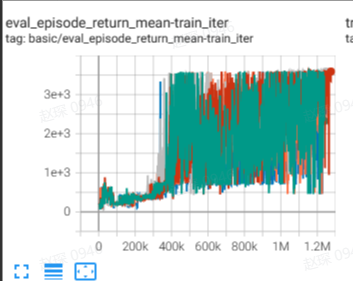
Hopper (Medium Expert)	110.8 \(\pm\) 1.3		config_link_ho	EDAC Repo (110.7 \(\pm\) 0.1)

Specifically for each dataset, our implementation results are as follows:

environment	medium expert	medium
HalfCheetah	92.5 \(\pm\) 2.8	59.9 \(\pm\) 2.8
Hopper	110.8 \(\pm\) 1.3	100.5 \(\pm\) 1.6

P.S.：

1. The above results are obtained by running the same configuration on four different random seeds (0, 42, 88, 123, 16)

2. The above benchmark is for HalfCheetah-v2, Hopper-v2.

3. The comparison results above is obtained via the paper Uncertainty-Based Offline Reinforcement Learning with Diversified Q-Ensemble. The complete table is depicted below

   

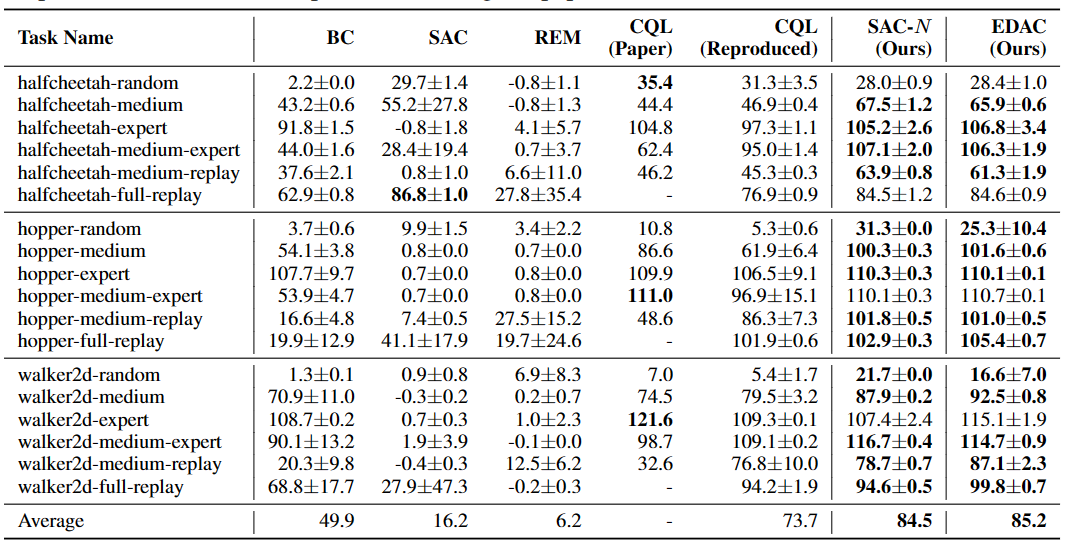
4. The above Tensorboard results illustrate the unnormalized results

Reference

• Kumar, Aviral, et al. “Conservative q-learning for offline reinforcement learning.” arXiv preprint arXiv:2006.04779 (2020).

• Chenjia Bai, et al. “Pessimistic Bootstrapping for Uncertainty-Driven Offline Reinforcement Learning.”

Other Public Implementations

• EDAC release repo