D4PG¶

Overview¶

D4PG, proposed in the paper Distributed Distributional Deterministic Policy Gradients, is an actor-critic, model-free policy gradient algorithm that extends upon DDPG. Improvements over DDPG include the use of N-step returns, prioritized experience replay and distributional value function. Moreover, training is parallelized with multiple distributed workers all writing into the same replay table. The authors found that these simple modifications contribute to the overall performance of the algorithm with N-step returns brining the biggest performance gain and priority buffer being the less crucial one.

Quick Facts¶

D4PG is only used for environments with continuous action spaces.(i.e. MuJoCo)
D4PG is an off-policy algorithm.
D4PG uses a distributional critic.
D4PG is a model-free and actor-critic RL algorithm, which optimizes actor network and critic network, respectively.
Usually, D4PG uses Ornstein-Uhlenbeck process or Gaussian process (default in our implementation) for exploration.

Key Equations or Key Graphs¶

The D4PG algorithm maintains a distributional critic \(Z_\pi(s, a)\) which estimates the expected Q value as a random variable such that \(Q(s, a)=\mathbb{E}Z_\pi(s, a)\). \(Z\) is usually a Categorical distribution over Q with 51 supports.

Accordingly, the distributional Bellman operator can be defined as:

\[\begin{aligned} (\mathcal{T}_{\pi} Z)(s, a)=r(s, a)+\gamma\mathbb{E}[Z(s',\pi(s'))|(s, a)] \end{aligned}\]

The distributional variant of the operator takes functions which map from state-action pairs to distributions, and returns a function of the same form. The loss used to learn the critic distribution parameters is defined as \(L(\pi) = \mathbb{E}[d(\mathcal{T}_{\pi_{\theta'}}, Z_{w'}(s, a), Z_{w}(s, a)]\) for some metric \(d\) that measures the distance between two distributions.

Finally, the actor update is done by taking the expectation with respect to the action-value distribution:

\[\begin{split}\begin{aligned} \nabla_\theta J(\theta) &\approx \mathbb{E}_{\rho^\pi} [\nabla_a Q_w(s, a) \nabla_\theta \pi_{\theta}(s) \rvert_{a=\pi\theta(s)}] \\ &= \mathbb{E}_{\rho^\pi} [\mathbb{E}[\nabla_a Z_w(s, a)] \nabla_\theta \pi_{\theta}(s) \rvert_{a=\pi\theta(s)}] \end{aligned}\end{split}\]

When calculating the TD error, D4PG computes N-step in the TD target to incorporate rewards in more future steps:

\[r(s_0, a_0) + \mathbb{E}[\sum_{n=1}^{N-1} \gamma^n r(s_n, a_n) + \gamma^N Q(s_N, \mu_\theta(s_N)) \vert s_0, a_0 ]\]

D4PG samples from a prioritized replay buffer with a non-uniform probability \(p_i\). This requires the use of importance sampling, implemented by weighting the critic update by a factor of \(R_{p_i}^{-1}\).

Note

D4PG utilizes multiple parallel independent actors, gathering experience and feeding data into the same replay buffer. However, our implementation only makes use of a single actor.

Pseudocode¶

../_images/D4PG_algo.png — source: https://lilianweng.github.io/posts/2018-04-08-policy-gradient/#d4pg¶

Implementations¶

The default config is defined as follows:

class ding.policy.d4pg.D4PGPolicy(cfg: EasyDict, model: Module | None = None, enable_field: List[str] | None = None)[source]

Overview:

Policy class of D4PG algorithm. D4PG is a variant of DDPG, which uses distributional critic. The distributional critic is implemented by using quantile regression. Paper link: https://arxiv.org/abs/1804.08617.

Property:

learn_mode, collect_mode, eval_mode

Config:

ID	Symbol	Type	Default Value	Description	Other(Shape)
1	`type`	str	d4pg	RL policy register name, refer to registry `POLICY_REGISTRY`	this arg is optional, a placeholder
2	`cuda`	bool	True	Whether to use cuda for network
3	`random_` `collect_size`	int	25000	Number of randomly collected training samples in replay buffer when training starts.	Default to 25000 for DDPG/TD3, 10000 for sac.
5	`learn.learning` `_rate_actor`	float	1e-3	Learning rate for actor network(aka. policy).
6	`learn.learning` `_rate_critic`	float	1e-3	Learning rates for critic network (aka. Q-network).
7	`learn.actor_` `update_freq`	int	1	When critic network updates once, how many times will actor network update.	Default 1
8	`learn.noise`	bool	False	Whether to add noise on target network’s action.	Default False for D4PG. Target Policy Smoo- thing Regularization in TD3 paper.
9	`learn.-` `ignore_done`	bool	False	Determine whether to ignore done flag.	Use ignore_done only in halfcheetah env.
10	`learn.-` `target_theta`	float	0.005	Used for soft update of the target network.	aka. Interpolation factor in polyak aver aging for target networks.
11	`collect.-` `noise_sigma`	float	0.1	Used for add noise during co- llection, through controlling the sigma of distribution	Sample noise from dis tribution, Gaussian process.
12	`model.v_min`	float	-10	Value of the smallest atom in the support set.
13	`model.v_max`	float	10	Value of the largest atom in the support set.
14	`model.n_atom`	int	51	Number of atoms in the support set of the value distribution.
15	`nstep`	int	3, [1, 5]	N-step reward discount sum for target q_value estimation
16	`priority`	bool	True	Whether use priority(PER)	priority sample, update priority

Model¶

Here we provide examples of QACDIST model as default model for D4PG.

class ding.model.template.qac_dist.QACDIST(obs_shape: int | SequenceType, action_shape: int | SequenceType, action_space: str = 'regression', critic_head_type: str = 'categorical', actor_head_hidden_size: int = 64, actor_head_layer_num: int = 1, critic_head_hidden_size: int = 64, critic_head_layer_num: int = 1, activation: Module | None = ReLU(), norm_type: str | None = None, v_min: float | None = -10, v_max: float | None = 10, n_atom: int | None = 51)[source]

Overview:: The QAC model with distributional Q-value.
Interfaces:: __init__, forward, compute_actor, compute_critic

compute_actor(inputs: Tensor) → Dict[source]

Overview:

Use encoded embedding tensor to predict output. Execute parameter updates with 'compute_actor' mode Use encoded embedding tensor to predict output.

Arguments:

inputs (torch.Tensor):
The encoded embedding tensor, determined with given hidden_size, i.e. (B, N=hidden_size). hidden_size = actor_head_hidden_size
mode (str): Name of the forward mode.

Returns:

outputs (Dict): Outputs of forward pass encoder and head.

ReturnsKeys (either):

action (torch.Tensor): Continuous action tensor with same size as action_shape.
logit (torch.Tensor):
Logit tensor encoding mu and sigma, both with same size as input x.

Shapes:

inputs (torch.Tensor): \((B, N0)\), B is batch size and N0 corresponds to hidden_size
action (torch.Tensor): \((B, N0)\)
logit (list): 2 elements, mu and sigma, each is the shape of \((B, N0)\).
q_value (torch.FloatTensor): \((B, )\), B is batch size.

Examples:

>>> # Regression mode
>>> model = QACDIST(64, 64, 'regression')
>>> inputs = torch.randn(4, 64)
>>> actor_outputs = model(inputs,'compute_actor')
>>> assert actor_outputs['action'].shape == torch.Size([4, 64])
>>> # Reparameterization Mode
>>> model = QACDIST(64, 64, 'reparameterization')
>>> inputs = torch.randn(4, 64)
>>> actor_outputs = model(inputs,'compute_actor')
>>> actor_outputs['logit'][0].shape # mu
>>> torch.Size([4, 64])
>>> actor_outputs['logit'][1].shape # sigma
>>> torch.Size([4, 64])

compute_critic(inputs: Dict) → Dict[source]

Overview:

Execute parameter updates with 'compute_critic' mode Use encoded embedding tensor to predict output.

Arguments:

obs, action encoded tensors.
mode (str): Name of the forward mode.

Returns:

outputs (Dict): Q-value output and distribution.

ReturnKeys:

q_value (torch.Tensor): Q value tensor with same size as batch size.
distribution (torch.Tensor): Q value distribution tensor.

Shapes:

obs (torch.Tensor): \((B, N1)\), where B is batch size and N1 is obs_shape
action (torch.Tensor): \((B, N2)\), where B is batch size and N2 is``action_shape``
q_value (torch.FloatTensor): \((B, N2)\), where B is batch size and N2 is action_shape
distribution (torch.FloatTensor): \((B, 1, N3)\), where B is batch size and N3 is num_atom

Examples:

>>> # Categorical mode
>>> inputs = {'obs': torch.randn(4,N), 'action': torch.randn(4,1)}
>>> model = QACDIST(obs_shape=(N, ),action_shape=1,action_space='regression',             ...                 critic_head_type='categorical', n_atoms=51)
>>> q_value = model(inputs, mode='compute_critic') # q value
>>> assert q_value['q_value'].shape == torch.Size([4, 1])
>>> assert q_value['distribution'].shape == torch.Size([4, 1, 51])

forward(inputs: Tensor | Dict, mode: str) → Dict[source]

Overview:

Use observation and action tensor to predict output. Parameter updates with QACDIST’s MLPs forward setup.

Arguments:

Forward with 'compute_actor':

inputs (torch.Tensor):
The encoded embedding tensor, determined with given hidden_size, i.e. (B, N=hidden_size). Whether actor_head_hidden_size or critic_head_hidden_size depend on mode.

Forward with 'compute_critic', inputs (Dict) Necessary Keys:

obs, action encoded tensors.

mode (str): Name of the forward mode.

Returns:

outputs (Dict): Outputs of network forward.
Forward with 'compute_actor', Necessary Keys (either):
action (torch.Tensor): Action tensor with same size as input x.

logit (torch.Tensor):
Logit tensor encoding mu and sigma, both with same size as input x.
Forward with 'compute_critic', Necessary Keys:
q_value (torch.Tensor): Q value tensor with same size as batch size.

distribution (torch.Tensor): Q value distribution tensor.

Actor Shapes:

inputs (torch.Tensor): \((B, N0)\), B is batch size and N0 corresponds to hidden_size
action (torch.Tensor): \((B, N0)\)
q_value (torch.FloatTensor): \((B, )\), where B is batch size.

Critic Shapes:

obs (torch.Tensor): \((B, N1)\), where B is batch size and N1 is obs_shape
action (torch.Tensor): \((B, N2)\), where B is batch size and N2 is``action_shape``
q_value (torch.FloatTensor): \((B, N2)\), where B is batch size and N2 is action_shape
distribution (torch.FloatTensor): \((B, 1, N3)\), where B is batch size and N3 is num_atom

Actor Examples:

>>> # Regression mode
>>> model = QACDIST(64, 64, 'regression')
>>> inputs = torch.randn(4, 64)
>>> actor_outputs = model(inputs,'compute_actor')
>>> assert actor_outputs['action'].shape == torch.Size([4, 64])
>>> # Reparameterization Mode
>>> model = QACDIST(64, 64, 'reparameterization')
>>> inputs = torch.randn(4, 64)
>>> actor_outputs = model(inputs,'compute_actor')
>>> actor_outputs['logit'][0].shape # mu
>>> torch.Size([4, 64])
>>> actor_outputs['logit'][1].shape # sigma
>>> torch.Size([4, 64])

Critic Examples:

>>> # Categorical mode
>>> inputs = {'obs': torch.randn(4,N), 'action': torch.randn(4,1)}
>>> model = QACDIST(obs_shape=(N, ),action_shape=1,action_space='regression',             ...                 critic_head_type='categorical', n_atoms=51)
>>> q_value = model(inputs, mode='compute_critic') # q value
>>> assert q_value['q_value'].shape == torch.Size([4, 1])
>>> assert q_value['distribution'].shape == torch.Size([4, 1, 51])

Benchmark¶

environment

best mean reward

evaluation results

config link

comparison

Halfcheetah

(Halfcheetah-v3)

13000

config_link_ha

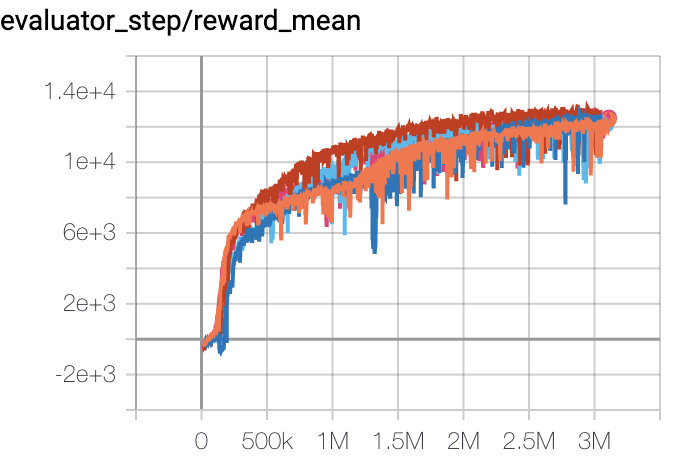
Walker2d

(Walker2d-v2)

5300

config_link_w

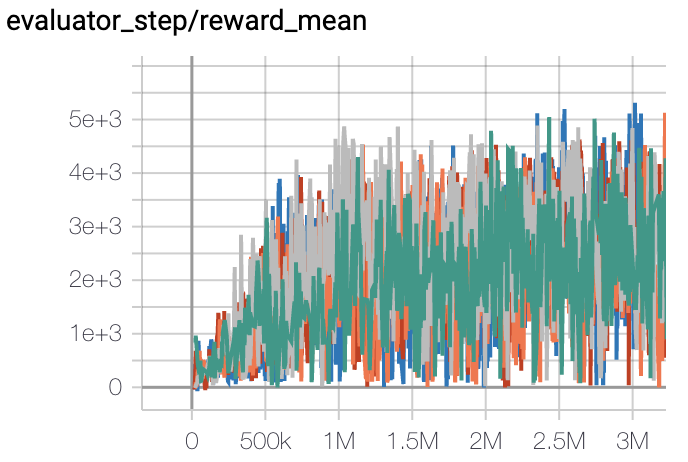
Hopper

(Hopper-v2)

3500

config_link_ho

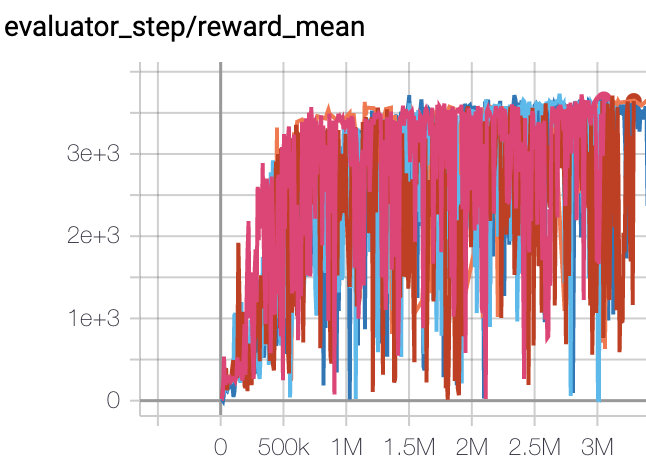
Other Public Implementations¶

D4PG Pytorch

References¶

Gabriel Barth-Maron, Matthew W. Hoffman, David Budden, Will Dabney, Dan Horgan, Dhruva TB, Alistair Muldal, Nicolas Heess, Timothy Lillicrap: “Distributed Distributional Deterministic Policy Gradients”, 2018; [https://arxiv.org/abs/1804.08617v1 arXiv:1804.08617v1].