PLR

概述

PLR 是在 Prioritized Level Replay 中提出的。 PLR是一种采样训练水平的方法，利用水平之间的学习潜力差异来提高样本效率和泛化能力。

核心要点

1. PLR 支持 多层次环境。

2. PLR 同时更新 策略 and 水平分数。

3. 在 DI-engine 的实现中，PLR与 PPG 算法相结合。

4. PLR 支持 Policy entropy, Policy min-margin, Policy least-confidence, 1-step TD error 和 GAE 得分函数。

关键框图

游戏关卡由随机种子确定，可以在导航布局、视觉外观和实体的起始位置方面有所变化。 PLR基于重播每个水平的预估学习潜力，有选择地采样下一个训练水平。下一个水平可以从支持未见过水平的分布中采样（顶部），这可能是环境的（可能是隐含的）完整训练水平分布，或者从重播分布中采样，该分布基于未来的学习潜力对水平进行优先排序（底部）。

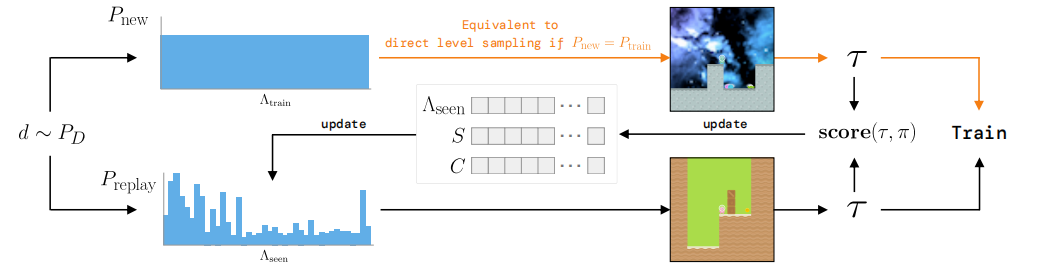
关键方程

学习潜力的得分水平是：

给定水平分数，我们使用在这些分数上评估并使用温度参数 $\beta$ 进行调整的优先级函数 $h$ 的归一化输出，以定义得分优先的分布 $P_S\left({\mathrm{\Lambda }}_{\text{train }}\right)$ ，用于对训练水平进行采样

$$P_S(l_i\mid {\mathrm{\Lambda }}_{\text{seen }},S)=\frac{h{\left(S_i\right)}^{1/\beta }}{\sum _{j}h{\left(S_j\right)}^{1/\beta }}$$

$$h\left(S_i\right)=1/\mathrm{rank}\left(S_i\right)$$

其中 $\mathrm{rank}\left(S_i\right)$ 是水平分数 $S_i$ 在按降序排序的所有分数中的排名。

由于用于参数化 $P_S$ 的分数是与策略状态相关联的，反映了越长时间没有通过重播进行更新，就越能逐渐反映出更“偏离策略”的度量。我们通过将采样分布明确与一个过时优先的分布 $P_C$ 混合，来缓解这种向 “off-policy-ness” 漂移的趋势：

$$P_C(l_i\mid {\mathrm{\Lambda }}_{\text{seen }},C,c)=\frac{c-C_i}{\sum _{C_j\in C}c-C_j}$$

$$P_{\text{replay }}\left(l_i\right)=(1-\rho )\cdot P_S(l_i\mid {\mathrm{\Lambda }}_{\text{seen }},S)+\rho \cdot P_C(l_i\mid {\mathrm{\Lambda }}_{\text{seen }},C,c)$$

伪代码

使用 PLR 的策略梯度训练循环

使用PLR进行经验采集

基准测试

Benchmark of PLR algorithm

environment	evaluation results	config link
BigFish		config_link_p

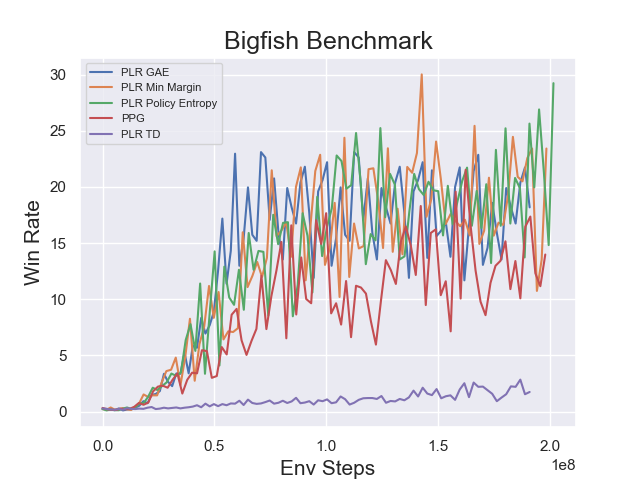
参考文献

Minqi Jiang, Edward Grefenstette, Tim Rocktaschel: “Prioritized Level Replay”, 2021; arXiv:2010.03934.

其他开源实现

• [facebookresearch](https://github.com/facebookresearch/level-replay)