SQL¶
概述¶
Soft Q Learning(SQL)是一种异策略(off-policy)的 maximum entropy Q learning 算法,首次在 Reinforcement Learning with Deep Energy-Based Policies 中被提出。 SQL 使用基于能量的模型,在其中通过最大化累积奖励的期望值加上熵项来学习通过玻尔兹曼分布表示的最优策略。 这样,最终得到的策略具有一种优势,即尝试学习执行任务的所有可能方式,而不仅仅是像其他传统强化学习算法那样只学习执行任务的最佳方式。 Stein variational gradient descent (SVGD) 被用于学习一个随机采样网络,该网络能够从策略的 energy-based model 中产生无偏样本。 该算法的特点包括通过最大熵公式改善探索能力,并具有可以在任务之间传递技能的组合性。
要点摘要¶
SQL 是一种 无模型(model-free) 和 基于值(value-based) 的强化学习算法。
SQL 是一种 异策略(off-policy) 算法。
SQL 同时支持 离散动作空间 和 连续动作空间 。
SVGD 已被采用于从具有 连续动作空间 的 soft Q 函数中进行采样。
关键方程或关键图表¶
SQL是一种最大熵策略的一种,这种策略(最大化熵策略)会选择一个使当前状态下概率最大的动作,同时最大化当前状态的不确定性或信息熵。 这有助于智能体平衡探索与利用,通过选择使得当前状态的不确定性最大的动作,来探索环境中未知的部分,并在已知部分利用已有的经验。 SQL考虑了一个更通用的最大熵策略,使得最优策略在每个访问的状态下都旨在最大化其熵值:
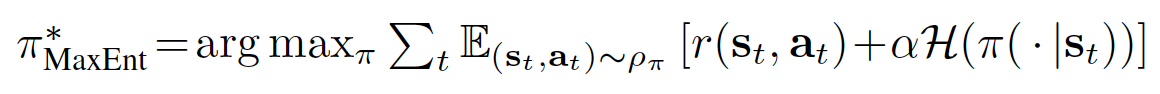
其中 \({\alpha}\) 是一个可选且方便的参数,可以用于确定熵和奖励的相对重要性。在实践中, \({\alpha}\) 是一个超参数,需要进行调优(不是在训练过程中学习得到的)。
通过下面的公式4和公式5定义 soft Q function 和 soft V function :
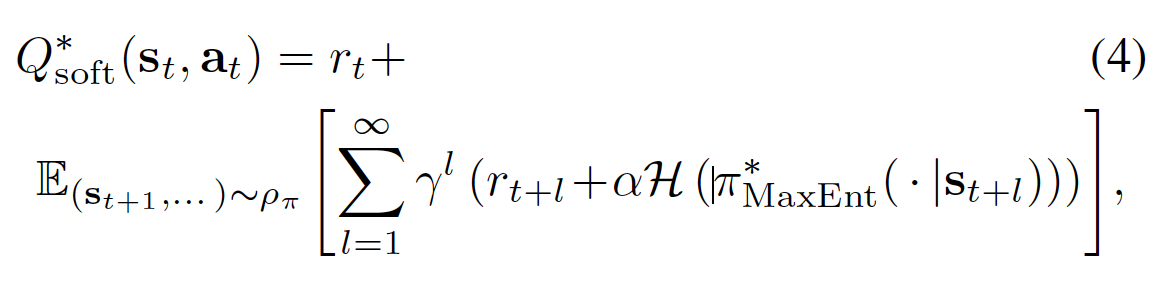
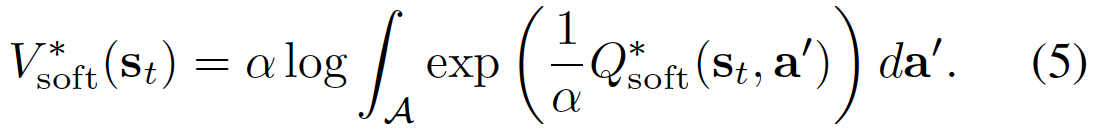
可以证明,对于上述基于最大熵公式的策略,最优策略为:
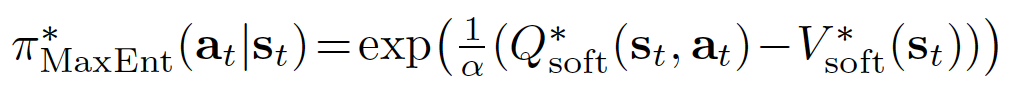
证明可以在附录中或者论文中找到 Modeling purposeful adaptive behavior with the principle of maximum causal entropy 。
用于训练富有表现力的 energy-based models 的 soft Q iteration 由以下定理给出: (Theorem 3 in the paper):
Theorem: Let \(Q_{\text{soft}(\cdot, \cdot))\) and \(V_{\text{soft}(\cdot))\) be bounded and assume that \(\int_{\mathcal{A}} exp(\frac{1}{\alpha} Q_{\text{soft}}(\cdot, a^{'}) ) \,da^{'} < \infty\) and that \(Q^{*}_{\text{soft}} < \infty\) exist. Then the fixed-point iteration
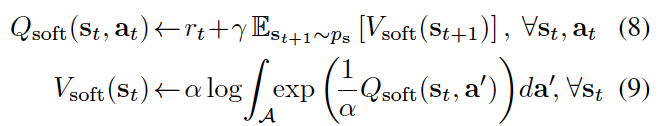
converges to \(Q^{*}_{\text{soft}} and V^{*}_{\text{soft}}\) respectively.
然而,为了将该算法应用于解决现实世界的问题,需要考虑几个实际问题。 首先,在连续的状态和动作空间中,以及在状态(或者)空间比较大的情况下,无法准确执行 soft Bellman backup ,其次,在一般情况下, 从energy-based models (公式6)中进行采样是难以处理的。
为了将上述定理转化为一个随机优化问题,我们首先通过重要性采样将 soft value function 表示为一个期望:
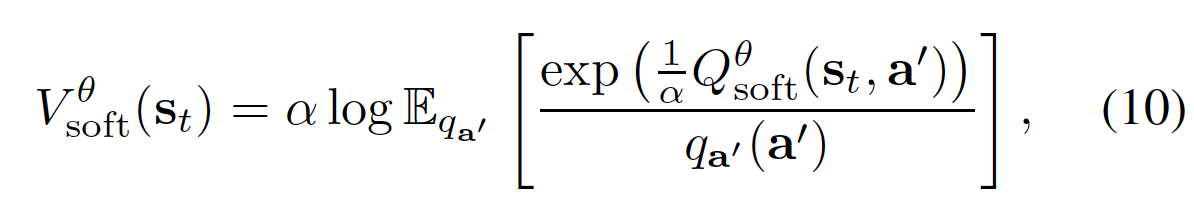
其中 \(q_{a'}\) 可是是动作空间中的任意分布。
考虑到以下等式: \(g_{1}(x)=g_{2}(x) \forall x \in \mathbb{X} \Leftrightarrow \mathbb{E}_{x\sim q}[((g_{1}(x)-g_{2}(x))^{2}]=0\) 其中, q 可以是在 \(\mathbb{X}\) 上的任意严格正的密度函数。 我们可以将 soft Q-iteration 表达为等价形式的最小化问题:
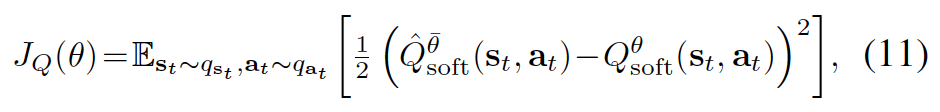
其中 \(q_{s_{t}}\) 和 \(q_{a_{t}}\) 在分别空间 \(\mathrm{S}\) 和 \(\mathrm{A}\) 是处处大于0的。
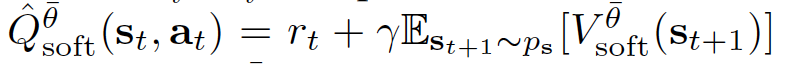
是 target Q-value, 其中 \(V^{\bar{\theta}}_{\text{soft}}\) 由公式 10 得到, 而 \(\theta\) 可以被目标参数 \(\bar{\theta}\) 所替代。
尽管采样的分布 \(q_{s_{t}}\), \(q_{a_{t}}\) and \(q_{a'}\) 可以是任意分布, 但我们通常使用当前策略的回放中的真实样本 \(\pi(a_{t}|s_{t}) \propto exp(\frac{1}{\alpha} Q_{\text{soft}}^{\theta}(s_{t},a_{t}))\).
然而,在连续空间中,由于策略的形式非常广泛,从中进行采样是困难的。 我们仍然需要一种可行的方式来从策略中进行采样。这就是SVGD发挥作用的地方。
形式上,我们希望学习一个基于状态条件的随机神经网络。 \(a_{t}=f^{\phi}(\xi,s_{t})\) 的参数是 \(\phi\), 它把标准高斯分布中(或者其他分布中)采样的噪声样本 \(\xi\) 映射到无偏的动作样本中。 我们将产生的动作分布表示为 \(\pi^{\phi}(a_{t}|s_{t})\) ,同时我们希望找到参数 \(\phi\) 使得产生的分布在 KL divergence 方面近似于 energy-based distribution 。
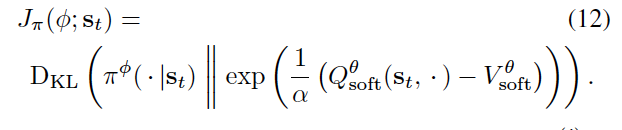
在实践中,我们通过以下两个方程来优化策略:
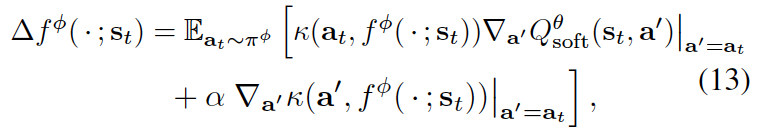
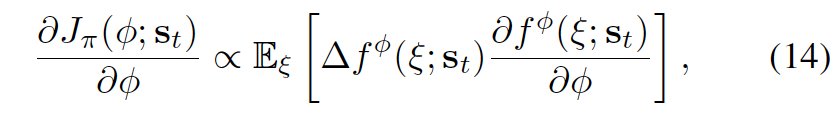
伪代码¶
伪代码如下所示:

其中,方程10、11、13和14可以从上述部分中参考。
扩展¶
SQL 可以与以下内容结合使用:
探索技术, 例如ε-贪婪或 OU 噪声 (这些技术可以在原始论文中找到;请参考 Continuous control with deep reinforcement learning 和 On the theory of the Brownian motion) 以增强探索能力。
策略梯度算法,一些分析人士将 Soft Q-learning 与策略梯度算法(Policy Gradient algorithms)之间建立了联系,比如 Equivalence Between Policy Gradients and Soft Q-Learning 。
演示数据, SQL可以与演示数据结合使用,用于提出一种模仿学习算法: SQIL, 该算法在以下论文中提出: SQIL: Imitation Learning via Reinforcement Learning with Sparse Rewards 。 请参考 DI-engine 实现中的 SQIL 代码,链接: SQIL code 。
实现¶
默认配置被定义如下:
- class ding.policy.sql.SQLPolicy(cfg: EasyDict, model: Module | None = None, enable_field: List[str] | None = None)[source]
- Overview:
Policy class of SQL algorithm.
基准¶
下表显示了DQN、SQL(在离散动作空间中)和SQIL在Lunarlander和Pong环境中的性能基准测试结果。
env / method |
DQN |
SQL |
SQIL |
alpha |
|---|---|---|---|---|
LunarLander |
153392 / 277 / 23900 (both off) 83016 / 155 / 12950 (both on) |
693664 / 1017 / 32436 (both off) 1149592 / 1388/ 53805 (both on) |
35856 / 238 / 1683 (both off) 31376 / 197 / 1479 (both on) |
0.08 |
Pong |
765848 / 482 / 80000 (both on) |
2682144 / 1750 / 278250 (both on) |
2390608 / 1665 / 247700 (both on) |
0.12 |
Note
Lunarlander和Pong的停止值分别为200和20, 当评估值的平均值到达停止值以上的时候训练停止。
参考文献¶
Haarnoja, Tuomas, et al. “Reinforcement learning with deep energy-based policies.” International Conference on Machine Learning. PMLR, 2017.
Uhlenbeck, G. E. and Ornstein, L. S. On the theory of the brownian motion. Physical review, 36(5):823, 1930.
Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T., Tassa, Y., Silver, D., and Wierstra, D. Continuous control with deep reinforcement learning. arXiv preprint arXiv:1509.02971, 2015.
Schulman, John, Xi Chen, and Pieter Abbeel. “Equivalence between policy gradients and soft q-learning.” arXiv preprint arXiv:1704.06440 (2017).
Siddharth Reddy, Anca D. Dragan, Sergey Levine: “SQIL: Imitation Learning via Reinforcement Learning with Sparse Rewards”, 2019.
Ziebart, B. D. Modeling purposeful adaptive behavior with the principle of maximum causal entropy. PhD thesis, 2010.