Table of Contents
Shortcuts

Ising Model

概述

伊辛模型 (Ising Model) 是一种经典的物理模型，用于描述铁磁性材料的微观磁态。在本环境中，该模型被扩展为一个多智能体系统，每个智能体通过局部交互影响整体系统的磁态。智能体的目标是通过改变自身的自旋状态来优化整个系统的有序性。

环境介绍

动作空间

在 Ising Model 环境中，每个智能体的动作空间是离散的，并且由两种可能的动作组成：

  • 保持自旋状态不变（通常表示为0）。

  • 改变自旋状态（通常表示为1）。

使用 gym 环境空间定义则可表示为：

from gym import spaces

action_space = gym.spaces.Discrete(2)

状态空间

状态空间由每个智能体的自旋状态和其观察到的邻居智能体的自旋状态组成。每个智能体的自旋状态可以是+1（向上）或-1（向下）。智能体的观察由 view_sight 属性定义，该属性决定了智能体可以观察到的邻居范围。

状态空间可以表示为一个二维数组，其中每个元素对应一个智能体的自旋状态。智能体的局部状态由其 IsingAgentState 对象表示，而全局状态由 IsingWorld 对象的 global_state 属性给出。

奖励空间

在本环境中，奖励是基于智能体自旋状态与邻居自旋状态的一致性。具体来说，奖励计算如下：

  • 对于每个智能体 i，计算其邻居的自旋状态的平均值。

  • 智能体 i 的奖励是其自旋状态与邻居自旋状态平均值的乘积的负数。

  • 奖励的设计鼓励智能体采取行动，以增加系统的总体有序性。

# 对于某一个智能体 agent：
reward = - 0.5 * global_state[agent.state.p_pos] * np.sum(global_state.flatten() * agent.spin_mask)

终止条件

遇到以下任何一种情况，则环境会该认为当前 episode 终止：

  • 达到 episode 的最大上限步数（默认设置为200）

  • 当全局序参数 order_param 达到1时，表示系统已经达到完全有序的状态，此时认为环境任务完成，游戏结束。序参数是系统自旋向上和自旋向下的智能体数量差的绝对值，除以总智能体数量。

    • 具体来说，序参数可以定义为系统中自旋向上的粒子数与总粒子数之差，除以总粒子数，即： \(Order Parameter = \frac{N_{up} - N_{down}} {N_{total}}\)

    • 其中， \(N_{\text{up}}\) 是自旋向上的粒子数， \(N_{\text{down}}\) 是自旋向下的粒子数， \(N_{\text{total}}\) 是系统中的总粒子数。

Mean field MARL

Mean Field 近似

Mean field 近似（见 Phase Transitions and Critical Phenomena ）是一种数学和统计物理中的方法，用于近似描述大量相互作用粒子的系统。在这种近似中，每个粒子被假设只受到其他所有粒子的平均效应的影响，而不是受到每个单独粒子的影响。这种方法可以简化复杂系统的计算，使得分析和优化变得更加可行。

Mean Field MARL 算法

Mean field MARL （见论文 Mean Field Multi-Agent Reinforcement Learning ）算法将 Mean Field 近似的思想应用到多智能体强化学习中。在这种算法中，每个智能体在做出决策时，不再考虑其他所有智能体的个体行为，而是假设其他智能体的行为可以用一个平均场（Mean Field）来表示。这个平均场代表了环境中所有其他智能体的行为分布。

Mean field MARL 算法主要解决的是集中式多智能体强化学习中，联合动作 \(a\) 的维度随智能体数量n的增多极速扩大的情况。因为每个智能体是同时根据联合策略估计自身的值函数，因此当联合动作空间很大时，学习效率及学习效果非常差。为了解决这个问题，算法将值函数 \(Q_\pi^j(s,a)\) 转化为只包含邻居之间相互作用的形式：

\[Q_j(s,a)=\frac{1}{N_j}\sum_{k\in N(j)}Q_j(s,a_j,a_k)\qquad (1)\]

其中 \(N(j)\) 表示智能体 j 邻居智能体的标签集， \(N_j=|N(j)|\) 表示邻居节点的个数。上式(4)对智能体之间的交互作用进行了一个近似，降低了表示智能体交互的复杂度，并且保留了部分主要的交互作用（近似保留邻居之间的交互，去掉了非邻居之间的交互）。虽然对联合动作 \(a\) 做了近似化简，但是状态信息 \(s\) 依然是一个全局信息。

将平均场论的思想引入式(1)中。该算法假定所有智能体都是同构的，其动作空间相同，并且动作空间是离散的。 每个智能体的动作采用 one-hot 编码方式， 如智能体j的动作 \(a_j=[a_j^1,a_j^2,\cdots,a_j^D]\) 表示共有D个动作的动作空间每个动作的值，若选取动作 \(i\)， 则 \(a_j^i=1\) ，其余为0。 定义 \(\overline a_j\) 为智能体 \(j\) 邻居 \(N(j)\) 的平均动作，其邻居 \(k\) 的 one-hot 编码动作 \(a_k\) 可以表示为 \(\overline a_j\) 与一个波动 \(\delta a_{j,k}\) 的形式

\[a_k=\overline a_j+\delta a_{j,k}, \qquad {\rm where}\ \overline a_j=\frac{1}{N_j}\sum_k a_k \qquad (2)\]

泰勒公式展开(1):

\[\begin{split}\begin{aligned} Q_j(s,a)&=\frac{1}{N_j}\sum_{k\in N(j)}Q_j(s,a_j,a_k)\\ &=\frac{1}{N_j}\sum_k[Q_j(s,a_j,\overline a_j)+\nabla_{\widetilde a_{j,k}}Q_j(s,a_j,\overline a_j)\delta a_{j,k}+\frac{1}{2}\delta a_{j,k}\nabla_{\widetilde a_{j,k}}^2Q_j(s,a_j,\overline a_j)\delta a_{j,k}]\\ &=Q_j(s,a_j,\overline a_j)+\nabla_{\widetilde a_{j,k}}Q_j(s,a_j,\overline a_j)[\frac{1}{N_j}\sum_k\delta a_{j,k}]+\frac{1}{2N_j}\sum_k[\delta a_{j,k}\nabla_{\widetilde a_{j,k}}^2Q_j(s,a_j,\overline a_j)\delta a_{j,k}]\qquad (3)\\ &=Q_j(s,a_j,\overline a_j)+\frac{1}{2N_j}\sum_k R_{s,j}(a_k)\\ &\approx Q_j(s,a_j,\overline a_j)\qquad (4) \end{aligned}\end{split}\]

式(3)中第二项求和为0，可以直接化简掉，第三项为泰勒展开中的二阶项 \(R_{s,j}(a_k)\) 是一个随机变量。具有如下性质：若值函数 \(Q_j(s,a_j,a_k)\) 是一个 M-smooth 函数（M阶导数连续），则 \(R_{s,j}(a_k)\in [-2M,-2M]\) ，该性质在原文中给出了证明。

根据式(3)，将式(1)两两作用求和的形式进一步化简为中心智能体j与一个虚拟智能体 \(\overline a_j\) 的相互作用，虚拟智能体是智能体 j 所有邻居作用效果的平均。 因此得到 MF-Q 函数 \(Q_j(s,a_j,\overline a_j)\)。 假设有一段经验 \([s,\{a_j\},\{r_j\},s']\) ，MF-Q 可以通过下式循环更新:

\[Q_{j,t+1}(s,a_j,\overline a_j)=(1-\alpha)Q_{j,t}(s,a_j,\overline a_j)+\alpha[r_j+\gamma v_{j,t}(s')]\qquad (5)\]

Mean Field MARL 算法在 Ising Model 环境中的简单实现

我们利用了 DQN 的算法流程和网络结构，只在环境返回的 obs 上做出了改动，即将 agent 周围的邻居的上一步动作的 one-hot 编码平均作为 obs 的一部分和原有 obs 拼接作为新的 obs。

具体来说，我们在 IsingModelEnv` 的 calculate_action_prob` 方法中计算了每个智能体的邻居的平均动作，并将其与原始观察值拼接在一起。这样，我们就可以将原始观察值和邻居的动作信息一起输入到神经网络中，以估计每个智能体的 Q 值。

class IsingModelEnv(BaseEnv):
    ...
    def calculate_action_prob(self, actions):
        num_action = self._action_space.n
        N = actions.shape[0]  # agent_num
        # Convert actions to one_hot encoding
        one_hot_actions = np.eye(num_action)[actions.flatten()]
        action_prob = np.zeros((N, num_action))

        for i in range(N):
            # Select only the one_hot actions of agents visible to agent i
            visible_actions = one_hot_actions[self._env.agents[i].spin_mask == 1]
            if visible_actions.size > 0:
                # Calculate the average of the one_hot encoding for visible agents only
                action_prob[i] = visible_actions.mean(axis=0)
            else:
                # If no visible agents, action_prob remains zero for agent i
                action_prob[i] = np.zeros(num_action)

        return action_prob

    def step(self, action: np.ndarray) -> BaseEnvTimestep:
        ...
        # Calculate the average action of neighbors
        action_prob = self.calculate_action_prob(action)
        # Concatenate the average action of neighbors with the original observation
        obs = np.concatenate([obs, action_prob], axis=1)
        ...

DI-zoo 可运行代码示例

完整的训练配置文件在 github link 内，对于具体的配置文件，例如 gym_hybrid_ddpg_config.py ，使用如下命令即可运行：

python3 ./DI-engine/dizoo/ising_env/config/ising_mfq_config.py

基准算法性能

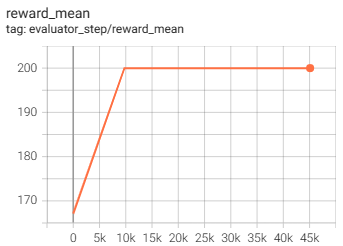
  • IsingModelEnv（50k env step 后停止，平均奖励等于 200 说明所有智能体选择了相同的方向，order_param 达到最大）

    • IsingModelEnv + Mean Field Q-learning:

    ../_images/ising_env.png