Table of Contents
Shortcuts

DT (DecisionTransformer)

综述

如果想要将强化学习技术应用在某个决策领域，最重要的就是将原始问题转换为一个合理的 MDP （马尔科夫决策过程）问题，而一旦问题环境本身有一些不那么友好的”特性“（比如部分可观测，非平稳过程等等），常规强化学习方法的效果便可能大打折扣。另一方面，随着近些年来数据驱动范式的发展，大数据和预训练大模型在计算机视觉（Computer Vision）和自然语言处理（Natural Language Processing）领域大放异彩，比如 CLIP，DALL·E 和 GPT-3 等工作都取得了惊人的效果，序列预测技术便是其中的核心模块之一。但对于决策智能，尤其是强化学习（Reinforcement Learning），由于缺少类似 CV 和 NLP 中的大数据集和适合的预训练任务，决策大模型迟迟没有进展。

在这样的背景下，为了推进决策大模型的发展，提高相关技术的实际落地价值，许多研究者开始关注 Offline RL/Batch RL 这一子领域。具体来说，Offline RL是一种只通过离线数据集（Offline dataset）训练策略（Policy），在训练过程中不与环境交互的强化学习任务。那对于这样的任务，是否可以借鉴 CV 和 NLP 领域的一些研究成果，比如序列预测相关技术呢？

于是乎，在2021年，以 Decision Transformer[3]/Trajectory Transformer[1-2]为代表的一系列工作出现了，试图将决策问题归于序列预测，将 transformer 结构应用在RL任务上，同时与语言模型，如 GPT-x 和 BERT 等联系起来。不像传统 RL 中计算 value 函数或计算 policy 梯度， DT 通过一个屏蔽后序的 transformer 直接输出最有动作选择。通过指定期望模型达到的reward，同时借助 states 和 actions 信息，就可以给出下一动作并达到期望的 reward。 DT 的达到并超过了 SOTA model-free offline RL 算法在 Atari，D4RL (MuJoCo) 等环境上的效果。

快速了解

  1. DT 是一个 offline 强化学习算法。

  2. DT 支持 离散（discrete） 和 连续（continuous） 动作空间。

  3. DT 使用 transformer 进行动作预测，但是对 self-attention 的结构进行了修改。

  4. DT 的数据集结构是由算法特点决定的，在进行模型训练和测试中都要符合其要求。

重要公示/重要图示

DT 的结构图如下：

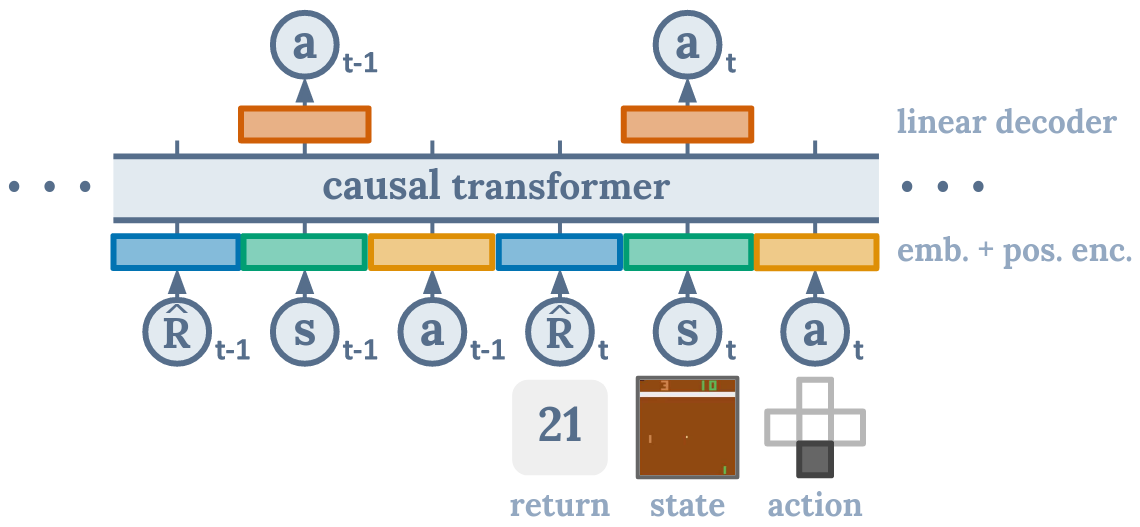
../_images/DT.png

图示说明 DT 算法在进行动作 at 的预测时，仅与当前时间步的 rt 和 st 以及之前的 rt-n, st-n, at-n 相关，与之后的无关， causal transformer 就是用来实现这一效果的模块。

伪代码

../_images/DT_algo.png

实现

DQNPolicy 的默认 config 如下所示：

class ding.policy.DTPolicy(cfg: EasyDict, model: Module | None = None, enable_field: List[str] | None = None)[source]
Overview:

Policy class of Decision Transformer algorithm in discrete environments. Paper link: https://arxiv.org/abs/2106.01345.

其中使用的神经网络接口如下所示：

class ding.model.DecisionTransformer(state_dim: int | SequenceType, act_dim: int, n_blocks: int, h_dim: int, context_len: int, n_heads: int, drop_p: float, max_timestep: int = 4096, state_encoder: Module | None = None, continuous: bool = False)[source]
Overview:

The implementation of decision transformer.

Interfaces:

__init__, forward, configure_optimizers

forward(timesteps: Tensor, states: Tensor, actions: Tensor, returns_to_go: Tensor, tar: int | None = None) → Tuple[Tensor, Tensor, Tensor][source]
Overview:

Forward computation graph of the decision transformer, input a sequence tensor and return a tensor with the same shape.

Arguments:

  • timesteps (torch.Tensor): The timestep for input sequence.

  • states (torch.Tensor): The sequence of states.

  • actions (torch.Tensor): The sequence of actions.

  • returns_to_go (torch.Tensor): The sequence of return-to-go.

  • tar (Optional[int]): Whether to predict action, regardless of index.

Returns:

  • output (Tuple[torch.Tensor, torch.Tensor, torch.Tensor]): Output contains three tensors, they are correspondingly the predicted states, predicted actions and predicted return-to-go.

Examples:
>>> B, T = 4, 6
>>> state_dim = 3
>>> act_dim = 2
>>> DT_model = DecisionTransformer(                state_dim=state_dim,                act_dim=act_dim,                n_blocks=3,                h_dim=8,                context_len=T,                n_heads=2,                drop_p=0.1,            )
>>> timesteps = torch.randint(0, 100, [B, 3 * T - 1, 1], dtype=torch.long)  # B x T
>>> states = torch.randn([B, T, state_dim])  # B x T x state_dim
>>> actions = torch.randint(0, act_dim, [B, T, 1])
>>> action_target = torch.randint(0, act_dim, [B, T, 1])
>>> returns_to_go_sample = torch.tensor([1, 0.8, 0.6, 0.4, 0.2, 0.]).repeat([B, 1]).unsqueeze(-1).float()
>>> traj_mask = torch.ones([B, T], dtype=torch.long)  # B x T
>>> actions = actions.squeeze(-1)
>>> state_preds, action_preds, return_preds = DT_model.forward(                timesteps=timesteps, states=states, actions=actions, returns_to_go=returns_to_go            )
>>> assert state_preds.shape == torch.Size([B, T, state_dim])
>>> assert return_preds.shape == torch.Size([B, T, 1])
>>> assert action_preds.shape == torch.Size([B, T, act_dim])

实验 Benchmark

Benchmark and comparison of DT algorithm

environment

best mean reward (normalized)

evaluation results

config link

comparison
Hopper
(Hopper-medium)

0.753 +- 0.035

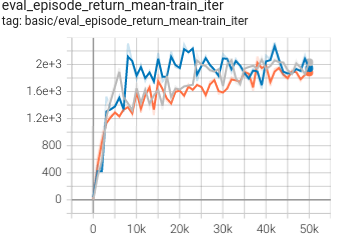
 ../_images/hopper_medium_dt.png

link_2_Hopper-medium

DT paper
Hopper
(Hopper-expert)

1.170 +- 0.003

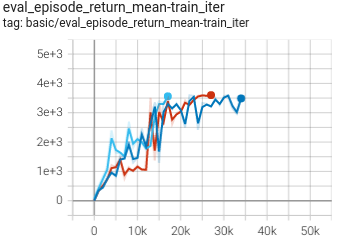
 ../_images/hopper_expert_dt.png

link_2_Hopper-expert

DT paper
Hopper
(Hopper-medium-replay)

0.651 +- 0.096

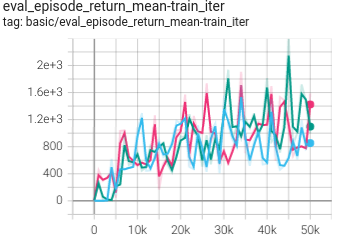
 ../_images/hopper_medium_replay_dt.png

link_2_Hopper-medium-replay

DT paper
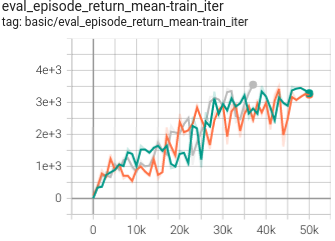
Hopper
(Hopper-medium-expert)

1.150 +- 0.016

 ../_images/hopper_medium_expert_dt.png

link_2_Hopper-medium-expert

DT paper
Walker2d
(Walker2d-medium)

0.829 +- 0.020

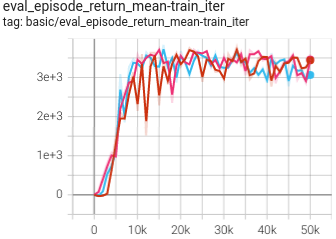
 ../_images/walker2d_medium_dt.png

link_2_Walker2d-medium

DT paper
Walker2d
(Walker2d-expert)

1.093 +- 0.004

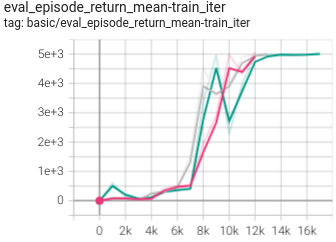
 ../_images/walker2d_expert_dt.png

link_2_Walker2d-expert

DT paper
Walker2d
(Walker2d-medium-replay)

0.603 +- 0.014

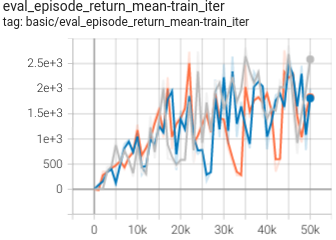
 ../_images/walker2d_medium_replay_dt.png

link_2_Walker2d-medium-replay

DT paper
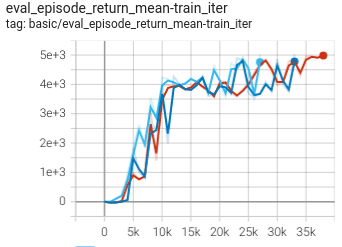
Walker2d
(Walker2d-medium-expert)

1.091 +- 0.002

 ../_images/walker2d_medium_expert_dt.png

link_2_Walker2d-medium-expert

DT paper
HalfCheetah
(HalfCheetah-medium)

0.433 +- 0.0007

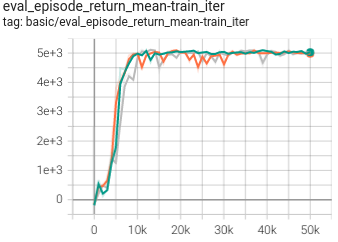
 ../_images/halfcheetah_medium_dt.png

link_2_HalfCheetah-medium

DT paper
HalfCheetah
(HalfCheetah-expert)

0.662 +- 0.057

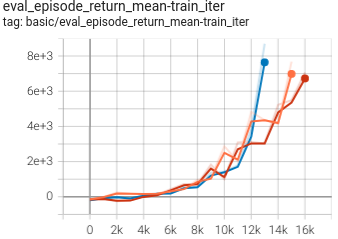
 ../_images/halfcheetah_expert_dt.png

link_2_HalfCheetah-expert

DT paper
HalfCheetah
(HalfCheetah-medium-replay)

0.401 +- 0.007

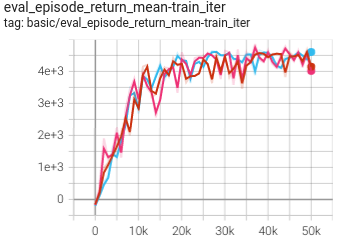
 ../_images/halfcheetah_medium_replay_dt.png

link_2_HalfCheetah-medium-replay

DT paper
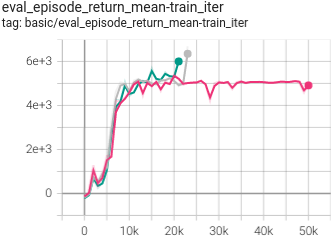
HalfCheetah
(HalfCheetah-medium-expert)

0.517 +- 0.043

 ../_images/halfcheetah_medium_expert_dt.png

link_2_HalfCheetah-medium-expert

DT paper
Pong
(PongNoFrameskip-v4)

0.956 +- 0.020

 ../_images/pong_dt.png

link_2_Pong

DT paper
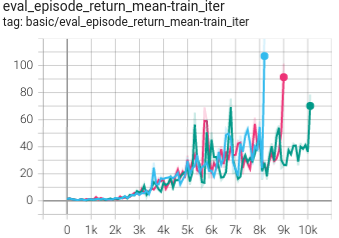
Breakout
(BreakoutNoFrameskip-v4)

0.976 +- 0.190

 ../_images/breakout_dt.png

link_2_Breakout

DT paper

注：

以上结果是在3个不同的随机种子（即123， 213， 321）运行相同的配置得到

参考文献