QGPO¶

概述¶

Q函数引导的策略优化算法，即 Q-Guided Policy Optimization(QGPO)，是由路橙、陈华玉等等，于2023年在论文《Contrastive Energy Prediction for Exact Energy-Guided Diffusion Sampling in Offline Reinforcement Learning》中提出，它是一种基于能量式条件扩散模型的 actor-critic 离线强化学习算法。

QGPO 算法由三个关键部分组成： 无条件扩散模型的行为策略 、 动作状态价值模型 ，以及 扩散中间态的能量模型 ，它用于引导最优策略的条件扩散模型的生成。

这三个模型的训练需要通过两个串行的步骤：首先通过使用离线数据集训练 无条件扩散模型的行为策略 直到收敛，随后交替训练 动作状态价值模型 与 扩散中间态的能量模型 直到收敛。

训练 动作状态价值模型 需要使用基于贝尔曼方程的训练目标。而为了训练 扩散中间态的能量模型 ，论文提出了能量条件扩散模型的新的训练目标，称之为对比能量预测 (CEP)。CEP 是一种对比学习目标，其关注的是在相同的状态行为搭配之间，最大化能量函数和能量引导的互信息。

核心要点¶

QGPO 是一种离线强化学习算法。
QGPO 是一种 Actor-Critic 强化学习算法。
QGPO 的 Actor 是基于无条件扩散模型与中间能量引导方程的能量式条件扩散模型。
QGPO 的 Critic 是基于能量函数的动作状态值函数。

关键方程或关键框图¶

使用 Kullback-Leibler 散度作为约束条件，对离线强化学习中的策略进行优化，可得最优策略 \(\pi^*\) 满足：

\[\begin{aligned} \pi^*(a|s) \propto \mu(a|s)e^{\beta Q_{\psi}(s,a)} \end{aligned}\]

其中 \(\mu(a|s)\) 是行为策略， \(Q_{\psi}(s,a)\) 是动作-状态价值函数，\(\beta\) 是温度系数的倒数。

它可被视为以 \(-Q_{\psi}(s,a)\) 为能量函数， \(\beta\) 为温度系数，关于动作 \(a\) 的 Boltzmann 分布。

如果以 \(x0\) 代替 \(a\) 写成一般形式，则目标分布为：

\[\begin{aligned} p_0(x_0) \propto q_0(x_0)e^{-\beta \mathcal{E}(x_0)} \end{aligned}\]

该分布可以由基于能量的条件扩散模型建模：

\[\begin{aligned} p_t(x_t) \propto q_t(x_t)e^{-\beta \mathcal{E}_t(x_t)} \end{aligned}\]

其中 \(q_t(x_t)\) 是无条件扩散模型， \(\mathcal{E}_t(x_t)\) 是扩散过程中的中间能量。

如果对扩散模型进行推断，该基于能量的条件扩散模型的得分函数可以计算为：

\[\begin{aligned} \nabla_{x_t} \log p_t(x_t) = \nabla_{x_t} \log q_t(x_t) - \beta \nabla_{x_t} \mathcal{E}_t(x_t) \end{aligned}\]

其中 \(\nabla_{x_t} \log q_t(x_t)\) 是无条件扩散模型的得分函数， \(\nabla_{x_t} \mathcal{E}_t(x_t)\) 是被命名为能量指导的中间能量的得分函数。

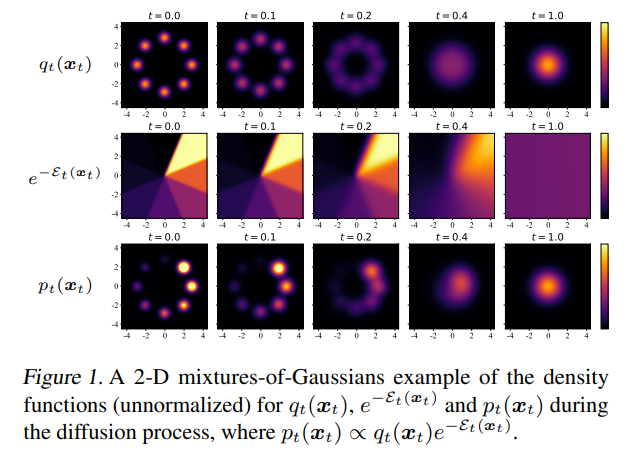
作为基于能量的条件扩散模型的策略，QGPO 包含三个组成部分：无条件扩散模型的行为策略，基于能量函数的动作状态价值函数和中间能量引导函数。

因此，QGPO 的训练有三个步骤：训练无条件扩散模型，训练能量函数并训练能量引导函数。

首先，无条件扩散模型通过最小化无条件扩散模型的负对数似然，在离线数据集上进行训练，这转变为最小化无条件扩散模型的得分函数的加权 MSE 损失：

\[\begin{aligned} \mathcal{L}_{\theta} = \mathbb{E}_{t,x_0,\epsilon} \left[ \left( \epsilon_{\theta}(x_t,t) - \epsilon \right)^2 \right] \end{aligned}\]

其中 \(\theta\) 是无条件扩散模型的系数。

在 QGPO 算法中，关于动作 \(a\) 的无条件扩散模型以状态 \(s\) 作为额外条件，它可以被写为：

\[\begin{aligned} \mathcal{L}_{\theta} = \mathbb{E}_{t,s,a,\epsilon} \left[ \left( \epsilon_{\theta}(a_t,s,t) - \epsilon \right)^2 \right] \end{aligned}\]

其中 \(x_0\) 是最初状态，\(x_t\) 是扩散过程经过时间 \(t\) 长度后的状态值。

其次，状态动作值函数可以通过 in-support softmax Q-Learning 方法计算：

\[\begin{split}\begin{aligned} \mathcal{T}Q_{\psi}(s,a) &= r(s,a) + \gamma \mathbb{E}_{s' \sim p(s'|s,a), a' \sim \pi(a'|s')} \left[ Q_{\psi}(s',a') \right] \\ &\approx r(s,a) + \gamma \frac{\sum_{\hat{a}}{e^{\beta_Q Q_{\psi}(s',\hat{a})}Q_{\psi}(s',\hat{a})}}{\sum_{\hat{a}}{e^{\beta_Q Q_{\psi}(s',\hat{a})}}} \end{aligned}\end{split}\]

其中 \(\psi\) 是动作状态值函数的参数， \(\hat{a}\) 是从无条件扩散模型采样的动作。

第三步，能量指导函数通过最小化对比能量预测(CEP)损失进行训练：

\[\begin{aligned} \mathcal{L}_{\phi} = \mathbb{E}_{t,s,\epsilon^{1:K},a^{1:K}\sim \mu(a|s)}\left[-\sum_{i=1}^{K}\frac{\exp(\beta Q_{\psi}(a^i,s))}{\sum_{j=1}^{K}\exp(\beta Q_{\psi}(a^j,s))}\log{\frac{\exp(f_{\phi}(a_t^i,s,t))}{\sum_{j=1}^{K}\exp(f_{\phi}(a_t^j,s,t))}}\right] \end{aligned}\]

其中 \(\phi\) 是能量指导函数的参数。

训练完毕后，QGPO 策略的动作生成是一个以当前状态为条件的扩散模型采样过程，可以通过联合使用无条件扩散模型建模的行为策略，和扩散中间态的能量模型的梯度作为能量引导函数来计算其得分函数：

\[\begin{aligned} \nabla_{a_t} \log p_t(a_t|s) = \nabla_{a_t} \log q_t(a_t|s) - \beta \nabla_{a_t} \mathcal{E}_t(a_t,s) \end{aligned}\]

随后使用 DPM-Solver 求解和采样该得分函数建模的扩散模型，得到最优动作：

\[\begin{split}\begin{aligned} a_0 &= \mathrm{DPMSolver}(\nabla_{a_t} \log p_t(a_t|s), a_1) \\ a_1 &\sim \mathcal{N}(0, I) \end{aligned}\end{split}\]

实现¶

该策略的默认配置如下：

class ding.policy.qgpo.QGPOPolicy(cfg: EasyDict, model: Module | None = None, enable_field: List[str] | None = None)[source]¶

Overview:: Policy class of QGPO algorithm (https://arxiv.org/abs/2304.12824). Contrastive Energy Prediction for Exact Energy-Guided Diffusion Sampling in Offline Reinforcement Learning
Interfaces:: __init__, forward, learn, eval, state_dict, load_state_dict

模型¶

支持 QGPO 算法的模型具有以下接口格式：

class ding.model.QGPO(cfg: EasyDict)[source]¶

Overview:: Model of QGPO algorithm.
Interfaces:: __init__, calculateQ, select_actions, sample, score_model_loss_fn, q_loss_fn, qt_loss_fn

__init__(cfg: EasyDict) → None[source]¶

Overview:

Initialization of QGPO.

Arguments:

cfg (EasyDict): The config dict.

_backward_hooks: Dict[int, Callable]¶

_backward_pre_hooks: Dict[int, Callable]¶

_buffers: Dict[str, Tensor | None]¶

_forward_hooks: Dict[int, Callable]¶

_forward_hooks_always_called: Dict[int, bool]¶

_forward_hooks_with_kwargs: Dict[int, bool]¶

_forward_pre_hooks: Dict[int, Callable]¶

_forward_pre_hooks_with_kwargs: Dict[int, bool]¶

_is_full_backward_hook: bool | None¶

_load_state_dict_post_hooks: Dict[int, Callable]¶

_load_state_dict_pre_hooks: Dict[int, Callable]¶

_modules: Dict[str, Module | None]¶

_non_persistent_buffers_set: Set[str]¶

_parameters: Dict[str, Parameter | None]¶

_state_dict_hooks: Dict[int, Callable]¶

_state_dict_pre_hooks: Dict[int, Callable]¶

calculateQ(s, a)[source]¶

Overview:

Calculate the Q value.

Arguments:

s (torch.Tensor): The input state.
a (torch.Tensor): The input action.

q_loss_fn(a, s, r, s_, d, fake_a_, discount=0.99)[source]¶

Overview:

The loss function for training Q function.

Arguments:

a (torch.Tensor): The input action.
s (torch.Tensor): The input state.
r (torch.Tensor): The input reward.
s_ (torch.Tensor): The input next state.
d (torch.Tensor): The input done.
fake_a (torch.Tensor): The input fake action.
discount (float): The discount factor.

qt_loss_fn(s, fake_a)[source]¶

Overview:

The loss function for training Guidance Qt.

Arguments:

s (torch.Tensor): The input state.
fake_a (torch.Tensor): The input fake action.

sample(states, sample_per_state=16, diffusion_steps=15, guidance_scale=1.0)[source]¶

Overview:

Sample actions for conditional sampling.

Arguments:

states (list): The input states.
sample_per_state (int): The number of samples per state.
diffusion_steps (int): The diffusion steps.
guidance_scale (float): The scale of guidance.

score_model_loss_fn(x, s, eps=0.001)[source]¶

Overview:: The loss function for training score-based generative models.
Arguments:: model: A PyTorch model instance that represents a time-dependent score-based model. x: A mini-batch of training data. eps: A tolerance value for numerical stability.

select_actions(states, diffusion_steps=15, guidance_scale=1.0)[source]¶

Overview:

Select actions for conditional sampling.

Arguments:

states (list): The input states.
diffusion_steps (int): The diffusion steps.
guidance_scale (float): The scale of guidance.

training: bool¶

Benchmark¶

QGPO 算法基线实验与对比¶
环境	最优平均回报	配置链接	对比
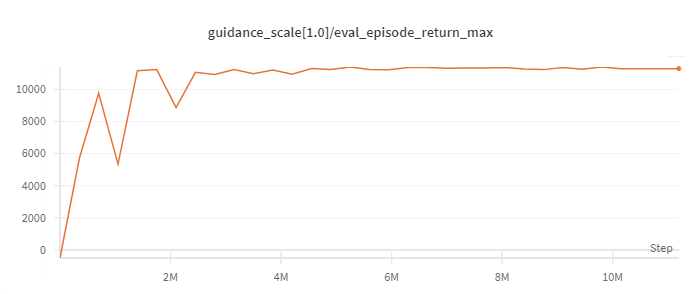
Halfcheetah (Medium Expert)	11226	config_link_1	d3rlpy(12124)
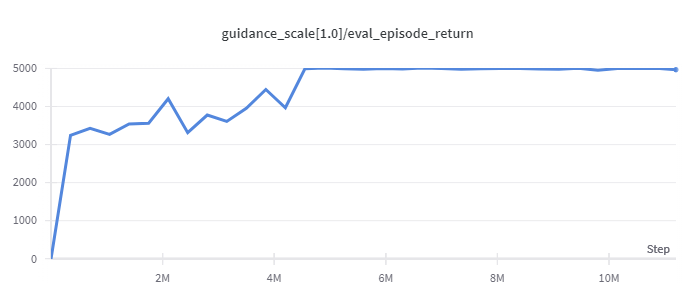
Walker2d (Medium Expert)	5044	config_link_2	d3rlpy(5108)
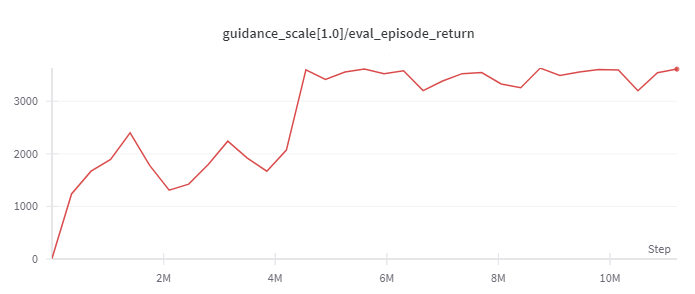
Hopper (Medium Expert)	3823	config_link_3	d3rlpy(3690)

Note: D4RL 环境基线实验可以在这里找到。

引用¶

Lu, Cheng, et al. “Contrastive Energy Prediction for Exact Energy-Guided Diffusion Sampling in Offline Reinforcement Learning.”, 2023; [https://arxiv.org/abs/2304.12824].

其他开源实现¶

Official implementation